Contrib:KeesWouters/staticshell
Contents
Static behaviour of rectangular plate
The dynamics of a rectangular plate can be predicted quite well with shell (coque_3d) elements. I also liked to know the accuracy of the displacements for this kind of structures. A comparison between solid elements and shell elements has been made.
Dimensions of the plate
The length and width of the plate are 1*1 m. The thickness of the shell elements has been increased to 0.02 m to enable meshing with solid elements (tetrahedrons and hexahedrons).
Boundary conditions and load
Two types of boundary conditions will be discussed:
- clamped at one side (all displacements and rotations are suppressed)
- [clamped at the four sides, tbd]
The load on the structure is a pressure of 0.1 bar on the surface of the plate.
Material properties
The Young's module and poisson ratio for steel are set to 210 GPa and 0.28.
Displacement at the tip using beam theory
According to the shell theory the displacement of a beam the tip under uniform pressure is:
- w = q*L^4/(8*D)
- uniform pressure q = 10 kPa
- length of plate L = 1 m
- Youngs' module E = 210 GPa
- poisson ratio nu = 0.28
- bending stiffness D = Eh^3/(12*(1-nu*nu)) = 151910 Nm and
- displacement at the tip w = 8.2286 mm
Salome model of the rectangular plate
Shell elements
The geometry and meshing follows the same procedure as for the dynamics: geometry of the plate and generating the mesh.
For a full description on shells see e.g Code Aster documentation (coque_3d).
Boundary conditions
For these calculations all the degree of freedoms (dofs) on one edge of the plate have been suppressed: three displacements and three rotations. This has been done in the corresponding comm file with the following rule:
clamped=AFFE_CHAR_MECA(MODELE=modelc,
DDL_IMPO=(_F(GROUP_MA=('Linex0',),
DX=0.0,
DY=0.0,
DZ=0.0,
DRX=0.0,
DRY=0.0,
DRZ=0.0,),),
FORCE_COQUE=_F(GROUP_MA='shell',
PRES=10.0e3,),);
The group Linex0, of course, defines one edge of the plate. The applied load FORCE_COQUE defines a surface load or pressure of 10 kPa on the group 'shell'.
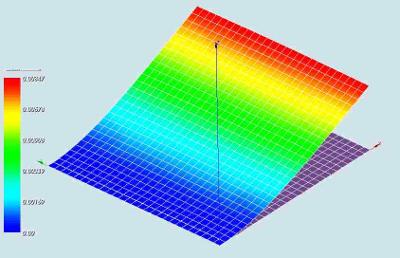
For this load case the calculated displacement at the tip of the plate is
w_ca = 8.460 mm for a mesh with 40 nodes (3*3 quad8/9 elements) and w_ca = 8.473 mm for a mesh with 2300 nodes.
In both cases this is slightly more than the theoretical value based on the shell theory: +2.8 % and +3.0 % for 40 and 2300 nodes respectively.
Comparison to solid elements
So it may be noted that the shell elements converge fairly rapidly to the correct value (here they even overestimate the displacement, can that be explained?). We expect that for solid elements convergence will be much slower.
In the graph below the results of some calculations are shown. We have used tetrahedron and hexahedron elements, both linear and quadratic.
On the x-axis the number of nodes (thousands of nodes) are given. They range from 40 for the shell mesh to nearly 150k for the solid elements. On the vertical axis the calculated displacement is given where the convergence value is about 0.0085 m.
Note that the 150k nodes is about the maximum my hardware is able to handle. It needs about 3.5 GB ram for this calculation and my physical limit is 4 GB now.
So it is fair to say that linear elements will be much too stiff for normal cases. Therefor the displacements of the structure will be predicted much too low. There has been a discussion about this many times on the CAElinux forums, but I didnot expect that linear elements give such a large stiffness compared to quadratic elements.
Mesh with solid elements
For comparison solid elements have been used to determine the behaviour of the plate.
It is easy in Salome to change from linear to quadratic elements: in the menu bar in the Mesh Module click on Modification-->Convert to/from quadratic or use the conversion icon on the top right. The you have the choice of converting to/from quadratic depending on the initial situation. Converting from linear to quadratic you also have the choice to place the medium node on the geometry: click the box medium nodes on geometry.
In most cases the calculation has been carried out with linear and quadratic elements using the same mesh grid. Saving the mesh into the med file after conversion is all that needs to be done. Starting the Code Aster calculations by ASTK is just hitting the run button if all file and directories are set.
Boundary conditions for the solid elements
Because the solid elements have no rotational degree of freedom the clamped edges must be given by fixed displacement of the side planes. The boundary conditions and loads are now defined in the comm file by:
clamp1=AFFE_CHAR_MECA(MODELE=ModQuad,
DDL_IMPO=(_F(GROUP_MA='f1',
DX=0.0,
DY=0.0,
DZ=0.0,),),
PRES_REP=_F(GROUP_MA='surfbot',
PRES=10000.0,),);
The group f1 is one of the side planes of the plate and all displacements on it are suppressed by the DDL_IMPO statement. The group 'surfbot' are all the shell elements.
The complete command file is given here: Media:commandfile.comm.zip
Hexahedron elements
The following python file defines the geometry and the mesh of the plate. The mesh consists of hexahedron elements. The number of nodes and elements is largely controlled by the parameter Mfineness at the start of the file. Currently set to 0.15 it yields exactly 30k nodes. The number of layer along the thickness of the plate is 4. Setting different values for Mfineness (in the range from 0.0 to 0.6) yields between 2 and 12 layers. For large number of nodes only linear elements can be solved due to lack of memory on my hardware.
Media:geom_mesh_solidplate.zip
Tetrahedron elements
Now change the meshing part in the python file to:
elemVol = 0.12
TMesh = smesh.Mesh(Extrusion1)
Tetrahedron_Netgen = TMesh.Tetrahedron(algo=smesh.NETGEN)
Max_Element_Volume = Tetrahedron_Netgen.MaxElementVolume(elemVol)
Max_Element_Volume.SetMaxElementVolume(elemVol)
smeshObj = smesh.smesh.CreateHypothesis('NETGEN_Parameters_2D','NETGENEngine')
Netgen_1D_2D = smesh.smesh.CreateHypothesis('NETGEN_2D','NETGENEngine')
status = TMesh.AddHypothesis(Netgen_1D_2D)
isDone = TMesh.Compute()
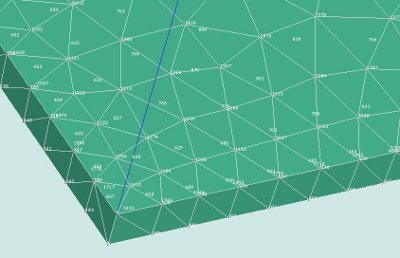
which basicly set the Netgen 3D and 2D parameters with the parameter elemVol. Setting elemVol=0.12 yields a linear mesh with 1.8k nodes with only one layer along the height of the plate, see picture.
the calculated stresses in the plate
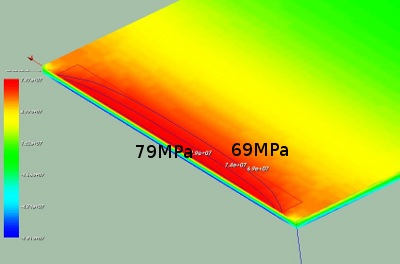
Using the solid elements it is easy to determine the relevant stresses in the plate. In the next picture the stress sigma_yy at the bottom of the plate (group surfbot in the Salome definition) are depicted. According to the theory this stress should be 75 MPa. In the calculation the stresses go up to nearly 80 MPa.
In the near future I will try to calculate the stresses with the shell elements and compare the results.
The stresses in the plate - hexahedron elements
Using the solid elements it is easy to determine the relevant stresses in the plate. In the next picture the stress sigma_yy at the bottom of the plate (the group surfbot in the Salome definition) are depicted. According to the theory this stress should be |sigma_yy| = 3*q/b*(L/h)^2 = 75 MPa. In the calculation the stresses go up to nearly 80 MPa.
The stresses in the plate - shell elements
Depending on which layer you would like to have the stresses, you need to define in the command file:
* for top layer NIVE_COUCHE='SUP' (superieur) * for centre layer NIVE_COUCHE='MOY' (moyenne) * for bottom layer NIVE_COUCHE='INF' (inferieur)
e.g to define the stresses in the top layer you can use the following sequence of commands:
# define top layer by 'SUP'
top=CALC_ELEM(REPE_COQUE=_F(NUME_COUCHE=1,NIVE_COUCHE='SUP',),
OPTION=('SIGM_ELNO_DEPL','EQUI_ELNO_SIGM',),
RESULTAT=result,);
....
top=CALC_NO(reuse=top,
RESULTAT=top,
OPTION='SIGM_NOEU_DEPL',);
...
# because Salome has a different mesh (quad8 iso coque_3d, quad9) we have to recalculate the stress fields to the initial Salome mesh
salomT=PROJ_CHAMP(RESULTAT=top,
MODELE_1=modelc, # project fields of this model to
MODELE_2=modinit,); # field of model_2
...
# and finally print the results.
# stresses in ['SUP', salomT, top], ['MOY', salomC, centre] and ['INF', salomB, bottom] layer,
# displacements in salomR
IMPR_RESU(FORMAT='MED',
UNITE=21,
RESU=(_F(MAILLAGE=meshinit,RESULTAT=salomT,
NOM_CHAM=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM','EQUI_ELNO_SIGM','DEPL','SIGM_ELNO_COQU',),),
_F(MAILLAGE=meshinit,RESULTAT=salomB,
NOM_CHAM=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM','EQUI_ELNO_SIGM','DEPL','SIGM_ELNO_COQU',),),
_F(MAILLAGE=meshinit,RESULTAT=salomC,
NOM_CHAM=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM','EQUI_ELNO_SIGM','DEPL','SIGM_ELNO_COQU',),),
_F(MAILLAGE=meshinit,RESULTAT=salomR,
NOM_CHAM=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM','EQUI_ELNO_SIGM','DEPL','SIGM_ELNO_COQU',),),),);
So also discussion here: http://www.code-aster.org/forum2/viewtopic.php?id=12523, help from, amoung others, Johannes Ackva and Thomas de Soza much appreciated.
The full command file is here: Media:kw_shell22.comm.zip
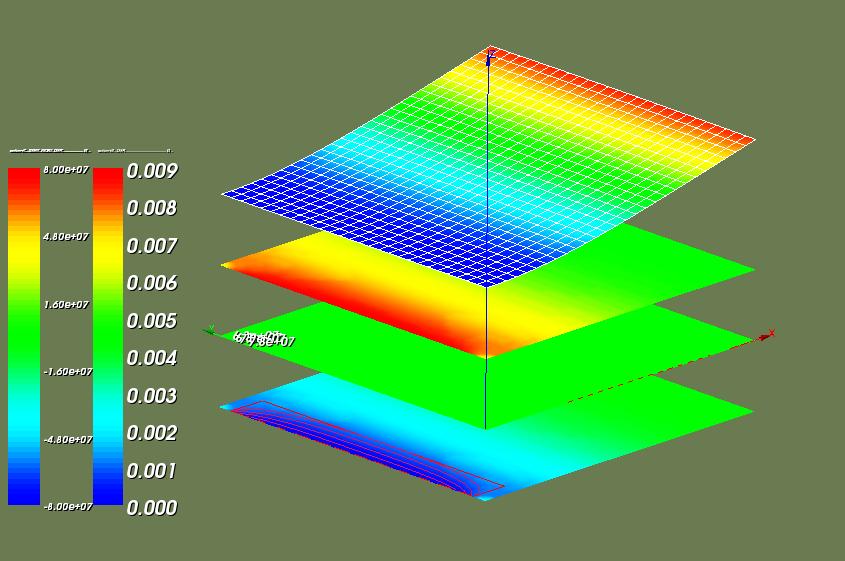
In the picture below the stresses are given in the three layers (bottom three fields). The displacement is given at the top.
In Salome a shift in z direction is given:
+0.4 for the displacement field. +0.2 for top stresses, 0.0 for centre stresses, -0.2 for bottom stresses,
The first legend in the picture indicates the stress, the second indicates the displacement in z direction.
Again the maximum absolute stress here is |sigma_xx| = 79 MPa, the same value that has been found by the hexahedron elements.
Remarks - notes - to do:
* [The labels of the stress values do not shift with the field somehow, so the values given in the centre layer belong to the bottom]
* [I am not sure whether all specified fields in the definition of the stresses are relevant/correct ('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM',
'EQUI_ELNO_SIGM','DEPL','SIGM_ELNO_COQU',), I do not have a complete overview of the exact meaning of every keyword. So if anybody is willing to give an update or link here, pls do]
* [still need to figure out to indicate the normal vector of each element, although this also may be pretty obvious.]
--kwarky 14:44, 7 May 2009 (CEST)