Contrib:KeesWouters/staticshell
Contents
Static behaviour of rectangular plate
The dynamics of a rectangular plate can be predicted quite well with shell (coque_3d) elements. I also liked to know the accuracy of the displacements for this kind of structures. A comparison between solid elements and shell elements has been made.
Dimensions of the plate
The length and width of the plate are 1*1 m. The thickness of the shell elements has been increased to 0.020 m to enable meshing with solid elements (tetrahedrons and hexahedrons).
Boundary conditions and load
Two types of boundary conditions will be discussed:
- clamped at one side (all displacements and rotations are suppressed)
- [clamped at the four sides, tbd]
The load on the structure is a pressure of 0.1 bar on the surface of the plate.
Material properties
The Young's module and poisson ratio for steel are set to 210 GPa and 0.28.
Displacement at the tip using beam theory
According to the shell theory the displacement of a beam the tip under uniform pressure is:
- w = q*L^4/(8*D)
- uniform pressure q = 10 kPa
- length of plate L = 1 m
- Youngs' module E = 210 GPa
- poisson ratio nu = 0.28
- bending stiffness D = Eh^3/(12*(1-nu*nu)) = 151910 Nm and
- displacement at the tip w = 8.2286 mm
Salome model of the rectangular plate
Shell elements
The geometry and meshing follows the same procedure as for the dynamics: geometry of the plate and generating the mesh.
For a full description on shells see e.g Code Aster documentation (coque_3d).
Boundary conditions
For these calculations all the degree of freedoms (dofs) on one edge of the plate have been suppressed: three displacements and three rotations. This has been done in the corresponding comm file with the following rule:
clamped=AFFE_CHAR_MECA(MODELE=modelc,
DDL_IMPO=(_F(GROUP_MA=('Linex0',),
DX=0.0,
DY=0.0,
DZ=0.0,
DRX=0.0,
DRY=0.0,
DRZ=0.0,),),
FORCE_COQUE=_F(GROUP_MA='shell',
PRES=10.0e3,),);
The group Linex0, of course, defines one edge of the plate. The applied load FORCE_COQUE defines a surface load or pressure of 10 kPa on the group 'shell'.
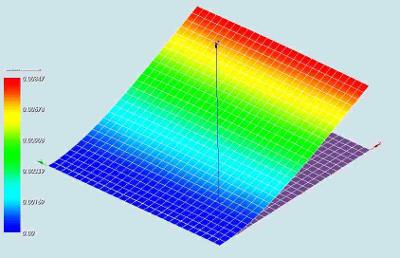
For this load case the calculated displacement at the tip of the plate is
w_ca = 8.460 mm for a mesh with 40 nodes (3*3 quad8/9 elements) and w_ca = 8.473 mm for a mesh with 2300 nodes.
In both cases this is slightly more than the theoretical value based on the shell theory: +2.8 % and +3.0 % for 40 and 2300 nodes respectively.
Comparison of displacement to solid elements
So it may be noted that the shell elements converge fairly rapidly to the correct value. We expect that for solid elements convergence will be much slower.
In the graph below the results of some calculations are shown. We have used tetrahedron and hexahedron elements, both linear and quadratic (tetra quad and hexa quad).
On the x-axis the number of nodes (thousands of nodes) are given. They range from 40 for the shell mesh to nearly 150k for the solid elements. On the vertical axis the calculated displacement is given where the convergence value is about 0.0085 m.
Note that the 150k nodes is about the maximum my hardware is able to handle. It needs about 3.5 GB ram for this calculation and my physical limit is 4 GB now.
So it is fair to say that linear elements will be much too stiff for normal cases. This has been discussed various times on the CAElinux forums.
General remarks with respect to element selection
From the graph it is clear that we should use quadratic elements as much as possible. Joël Cugnoni makes the following, more general statements (reference removed):
Concerning the choice of element / mesh refinement, here is a summary of my recommendations:
For 3D stress analysis in linear statics without contact:
- use quadratic elements by default: they will give you systematically better results than linear elements
- completely forget the linear tetrahedron, they are always too stiff and give bad stress predictions, their convergence rate is also very low (error does not change much if you refine the mesh)
- if you need to use linear elements: only use hexa or prisms. When bending is significant, put at least 2-4 linear elements through the thickness. To avoid "locking": try to keep the element aspect ratio between 1 and 5 or use reduced elements
For 3D stress analysis in non-linear statics & contact:
- in large strain analysis (plasticity), the enhanced accuracy of quadratic elements is usually less significant than in linear statics. The non-linear geometric effects and integration of local constitutive behaviour are more important. In this sense tetra are not the best choice in this case (strange plastic strain localization patterns...) My advice is to try several meshes and different element types (and exact/reduced integration). For highly non-linear studies, the best choice usually is a nice structured hexahedric mesh (linear or quadratic depending on the case)
- with contact, quadratic elements tend to have large contact pressure oscillation and may induce solver convergence problems. I would recommend to use a fine linear hexahedric (or at least prisms) mesh in this case
For 2D stress analysis:
- in linear statics, prefer quadratic elements
- for large strain / plasticity, try both and look which one is best
- (there are no really pathologic elements in 2D)
I hope that it will help you in your analysis - Joël
Table of results
The displacement at the tip for various numbers of nodes, number of layers over the thickness and different elements are given in the table below. This table has been used to compose the graph above.
mesh type w_ca Rel % KNodes layers
shell quad 0.008460 102.81 0.04
shell quad 0.008473 102.96 2.3
tetra LIN 0.001049 12.75 6 1
tetra LIN 0.002515 30.57 16 2
tetra LIN 0.003300 40.10 26 2
tetra Quad 0.008423 102.37 37 1
tetra Quad 0.008459 102.81 100 2
tetra Quad 0.008461 102.83 163 2
hexa LIN 0.001984 24.11 1 2
hexa LIN 0.004738 57.58 5 3
hexa LIN 0.005193 63.11 8 4
hexa LIN 0.006756 82.10 24 5
hexa LIN 0.007128 86.62 37 6
hexa LIN 0.007698 93.55 90 8
hexa LIN 0.007911 96.14 156 10
hexa Quad 0.008415 102.26 3.5 2 hexa Quad 0.008450 102.69 19 3 hexa Quad 0.008454 102.74 30 4 hexa Quad 0.008461 102.82 91 5 hexa Quad 0.008462 102.84 143 6
first and second column: mesh type: shell, hexahedron, tetrahedron, LINear or Quadratic third column: displacement at the tip [m] fourth column: relative displacement at the tip, compared to shell theory fifth column: number of nodes sixth column: number of layer along the thickness
Mesh with solid elements
For comparison solid elements have been used to determine the behaviour of the plate.
It is easy in Salome to change from linear to quadratic elements: in the menu bar in the Mesh Module click on Modification-->Convert to/from quadratic or use the conversion icon on the top right. The you have the choice of converting to/from quadratic depending on the initial situation. Converting from linear to quadratic you also have the choice to place the medium node on the geometry: click the box medium nodes on geometry.
In most cases the calculation has been carried out with linear and quadratic elements using the same mesh grid. Saving the mesh into the med file after conversion is all that needs to be done. Starting the Code Aster calculations by ASTK is just hitting the run button if all file and directories are set.
Boundary conditions for the solid elements
Because the solid elements have no rotational degree of freedom the clamped edges must be given by fixed displacement of the side planes. The boundary conditions and loads are now defined in the comm file by:
clamp1=AFFE_CHAR_MECA(MODELE=ModQuad,
DDL_IMPO=(_F(GROUP_MA='f1',
DX=0.0,
DY=0.0,
DZ=0.0,),),
PRES_REP=_F(GROUP_MA='surfbot',
PRES=10000.0,),);
The group f1 is one of the side planes of the plate and all displacements on it are suppressed by the DDL_IMPO statement. The group 'surfbot' include all the shell elements.
The complete command file is given here: Media:commandfile.comm.zip
Hexahedron elements
The following python file defines the geometry and the mesh of the plate. The mesh consists of hexahedron elements. The number of nodes and elements is largely controlled by the parameter Mfineness at the start of the file. Set this value to 0.15 and it yields exactly 30k nodes. The number of layer along the thickness of the plate is 4. Setting different values for Mfineness (in the range from 0.0 to 0.6) yields between 2 and 12 layers. For large number of nodes only linear elements can be solved due to lack of memory on my hardware.
mesh with Hexahedron elements
Tetrahedron elements
Now change the meshing part in the python file to:
elemVol = 0.12
TMesh = smesh.Mesh(Extrusion1)
Tetrahedron_Netgen = TMesh.Tetrahedron(algo=smesh.NETGEN)
Max_Element_Volume = Tetrahedron_Netgen.MaxElementVolume(elemVol)
Max_Element_Volume.SetMaxElementVolume(elemVol)
smeshObj = smesh.smesh.CreateHypothesis('NETGEN_Parameters_2D','NETGENEngine')
Netgen_1D_2D = smesh.smesh.CreateHypothesis('NETGEN_2D','NETGENEngine')
status = TMesh.AddHypothesis(Netgen_1D_2D)
isDone = TMesh.Compute()
which basicly set the Netgen 3D and 2D parameters with the parameter elemVol. Setting elemVol=0.12 yields a linear mesh with 1.8k nodes and only one layer along the height of the plate, see picture.
- mesh with tetrahedron elements
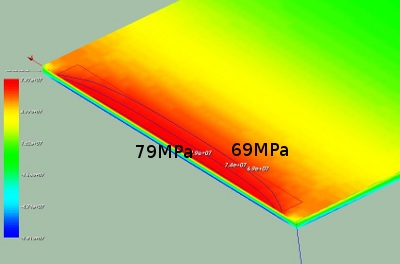
The stresses in the plate - hexahedron elements
Using the solid elements it is easy to determine the relevant stresses in the plate. In the next picture the stress sigma_yy at the bottom of the plate (the group surfbot in the Salome definition) are depicted. According to the theory this stress should be |sigma_yy| = 3*q/b*(L/h)^2 = 75 MPa. In the calculation the stresses go up to nearly 80 MPa.
The stresses in the plate - shell elements
Depending on which layer you would like to have the stresses, you need to define in the command file:
* for layer NIVE_COUCHE='SUP' (superieur, top) * for layer NIVE_COUCHE='MOY' (moyenne, center) * for layer NIVE_COUCHE='INF' (inferieur, bottom)
e.g to define the stresses in the top layer you can use the following sequence of commands:
# define top layer by 'SUP'
top=CALC_ELEM(REPE_COQUE=_F(NUME_COUCHE=1,NIVE_COUCHE='SUP',),
OPTION=('SIGM_ELNO_DEPL','EQUI_ELNO_SIGM',),
RESULTAT=result,);
....
top=CALC_NO(reuse=top,
RESULTAT=top,
OPTION='SIGM_NOEU_DEPL',);
...
# because Salome uses a different mesh (quad8 iso coque_3d/quad9) we have to project the stress fields to the initial Salome mesh *)
salomT=PROJ_CHAMP(RESULTAT=top,
MODELE_1=modelc, # project fields of this model to
MODELE_2=modinit,); # field of modele_2
...
# and finally print the results.
# stresses in ['SUP', salomT, top], ['MOY', salomC, centre] and ['INF', salomB, bottom] layer,
# displacements in salomR
IMPR_RESU(FORMAT='MED',
UNITE=21,
RESU=(_F(MAILLAGE=meshinit,RESULTAT=salomT,
NOM_CHAM=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM','EQUI_ELNO_SIGM','DEPL','SIGM_ELNO_COQU',),),
_F(MAILLAGE=meshinit,RESULTAT=salomB,
NOM_CHAM=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM','EQUI_ELNO_SIGM','DEPL','SIGM_ELNO_COQU',),),
_F(MAILLAGE=meshinit,RESULTAT=salomC,
NOM_CHAM=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM','EQUI_ELNO_SIGM','DEPL','SIGM_ELNO_COQU',),),
_F(MAILLAGE=meshinit,RESULTAT=salomR,
NOM_CHAM=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM','EQUI_ELNO_SIGM','DEPL','SIGM_ELNO_COQU',),),),);
- *) Added july 2010: In later versions op C-Aster (vs10.x) this in not necessary any more. You can directly write the results on a quadratic mesh (quad8 or tria6 elements). I have not tried linear elements.
See also discussion here: http://www.code-aster.org/forum2/viewtopic.php?id=12523. The contributions from, amoung others, Johannes Ackva and Thomas de Soza much appreciated.
The complete command file is here: Media:kw_shell22.comm.zip
Intermezzo: F_COPY_ERROR in CA10
You probably have to change the command file, line 23, command CREA_MAILLAGE(...) for Code Aster 10 and above, because no TRIA6 elements are available:
meshmod=CREA_MAILLAGE(MAILLAGE=meshinit,
MODI_MAILLE=(_F(TOUT='OUI',OPTION='QUAD8_9',),),);
##_F(TOUT='OUI',OPTION='TRIA6_7',),),); comment this out and add ,),); in previous line
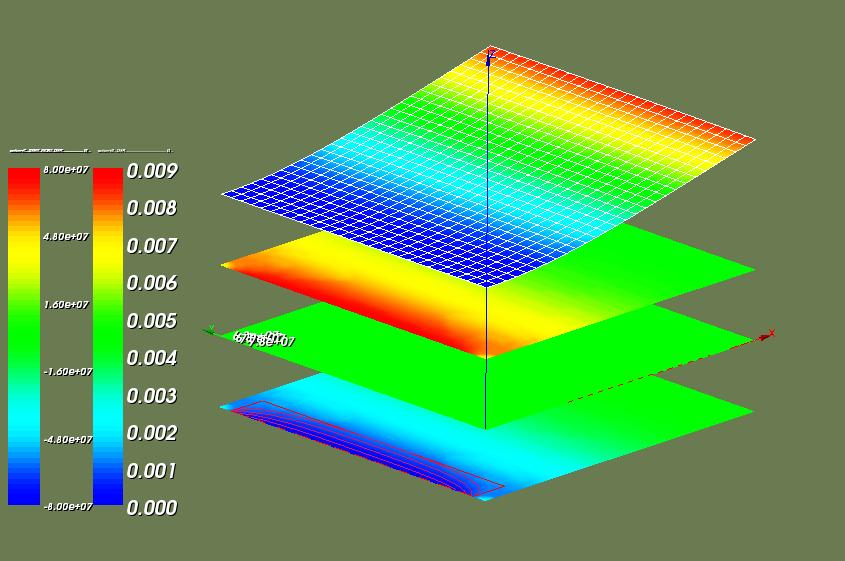
In the picture below the stresses are given in the three layers (bottom three fields). The displacement is given at the top.
In Salome a shift (Translate) in z direction is given:
top1: the displacement field.
top2: top stresses ('SUP'),
top3: centre stresses ('MOY'),
top4: bottom stresses ('INF'),
The first legend in the picture indicates the stress, the second indicates the displacement in z direction.
Again the maximum absolute stress here is |sigma_xx| = 79 MPa, the same value that has been found by the hexahedron elements.
Visualise the normal direction of the shells [Salome5.1.X]
In Salome version 5.1.x the the direction of the normals can be displayed in the shell mesh. Right click on the mesh, and tick Orientation of the faces. A small arrow appears and indicates the normal direction of the shells. This only works in Display mode --> shading, with or without shrink.
In this picture the normals of the greenish elements have been deliberately changed.
Note that in the geometry module it is also possible to show the normal to a plane by Measures --> Normal to face and select face and if necessary a point.
This feature is also availabel in Salome 4.x.
In this example, in the geometry module and the mesh module both (default) normals have the same direction.
Remarks - notes - to do
- [The labels of the stress values do not shift with the field somehow, so the values given in the centre layer belong to the bottom]
- [I am not sure whether all specified fields in the definition of the stresses are relevant/correct
- --- ('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM','EQUI_ELNO_SIGM','DEPL','SIGM_ELNO_COQU',),
- I do not have a complete overview of the exact meaning of every keyword. So if anybody is willing to give an update or link here, pls do]
(A limited list of CodeASter keywords is available at: http://www.code-aster.org/wiki/doku.php?id=en:p01_util:p120_terms)
- Use of DKT, DSG, Q4G and coque_3d, discussed here [Thomas DE SOZA]:
- DKT, DSG and Q4G as explained in U3.12.01 must use plane elements (that is for QUAD4 elements, all four nodes must be on a plane).
- COQUE_3D is the only shell element in Code_Aster that takes into account the curvature of the geometry (with quadratic elements).
- Moreover COQUE_3D supports non-linear geometry (large displacements, large rotations), but does not support large deformations.
- GREEN_GR enforces exact geometry but still implies a small deformation hypothesis (GREEN_GR is replaced by GDEP_GROT in CA10)
Writing results into a table or text file
In this section we will create tables and write the results to a text file. At the clamped area of the plate the nodal forces, reaction forces and stresses will be determined.
Results with solid elements
Nodal forces and reaction forces on the clamped area
The reaction forces can be written to a table in the same way as the mass of the plate. It mainly depends on the contribution of [Claus Andersen].
The additional commands that have been used are globally as follows:
- Calculate the reaction forces and nodal forces in a RESU file by adding the fields (champ) in the
- result=CALC_NO(...OPTION= (...,'FORC_NODA','REAC_NODA',...),);) command
- Define a nodal group, since the reaction forces needs to be determined from the node and cannot directly calculated from a mesh group group_ma(*): (???)
- MeshQuad=DEFI_GROUP(...).
Then create a table with arguments defining, among others:
- the nodal group,
- the name of the fields to determine the reaction forces and nodal forces (REAC_NODA and FORC_NODA) and
- a number of titles.
- TB_nodf=POST_RELEVE_T(...)
Finally print the table, defining:
- the unit to write to,
- the name of the table and
- format and titles
- IMPR_TABLE(...)
In more detail:
# we want to determine:
# nodal displacements - * - nodal forces - reaction forces
result=CALC_NO(reuse =result,
RESULTAT=result,
OPTION= ('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM','FORC_NODA','REAC_NODA',),);
...
#Define a group of nodes for 'reaction nodal force' retrieval:
# Use the mesh named 'mesh'
## [Create a mesh group called 'npf1' derived from group_ma='pf1']
## [Create a node group called 'npf1' ]
# Create a node group called 'npf1' dervied from group_ma='pf1'
MeshQuad=DEFI_GROUP(reuse =MeshQuad,
MAILLAGE=MeshQuad,
#[CREA_GROUP_MA=_F(NOM='npf1',GROUP_MA=('pf1',),),]
#[CREA_GROUP_NO=_F(GROUP_MA='npf1',),]
CREA_GROUP_NO=_F(NOM='npf1',GROUP_MA='pf1',),);
# determine a table for nodal reaction forces TB_nodf
# the values are stored in REAC_NODA and FORC_NODA fields (champ)
# the forces are determined on the clamped area (n)pf1
TB_nodf=POST_RELEVE_T(ACTION=(_F(OPERATION='EXTRACTION',
INTITULE='ReactionForces',
RESULTAT=result,
NOM_CHAM='REAC_NODA',
TOUT_ORDRE='OUI',
GROUP_NO='npf1',
RESULTANTE=('DX','DY','DZ',),
MOYE_NOEUD='NON',),
_F(OPERATION='EXTRACTION',
INTITULE='NodalForces',
RESULTAT=result,
NOM_CHAM='FORC_NODA',
PRECISION=0.000001,
GROUP_NO='npf1',
RESULTANTE=('DX','DY','DZ',),),),
TITRE='[Reaction] Nodal Forces',);
IMPR_TABLE(TABLE=TB_nodf,
FORMAT='TABLEAU',
UNITE=26,
SEPARATEUR=' ,',
TITRE='reaction forces at nodes on group 'npf1',);
In ASTK you need to define an output file with unit number 26. I followed Claus by giving the file a mast type and called the file 'table.txt'. See following screen shot:
It generates the following table in the text file:
# #--------------------------------------------------------------------------- # #reaction forces at nodes on group 'npf1' #[Reaction] Nodal Forces ,INTITULE ,RESU ,NOM_CHAM ,NUME_ORDRE ,INST ,DX ,DY ,DZ ,ReactionForces ,result ,REAC_NODA , 1 , 0.00000E+00 ,-1.43244E-06 ,-1.87237E-06 ,-1.00000E+04 ,NodalForces ,result ,FORC_NODA , 1 , 0.00000E+00 ,-1.43244E-06 ,-1.87237E-06 ,-9.95727E+03
The nodal forces FORC_NODA in z direction are about 4 % lower wrt (with respect to) the reaction forces. The pressure is 10 kPa on a 1*1 m2 surface, yielding exaclty 10 kN. The difference between nodal forces and reaction forces are the applied loads on the corresponding nodes:
REAC_NODA = FORC_NODA - applied load (REAC_NODA = FORC_NODA - chargements appliqués)
and is useful e.g. to verify the total applied loads (see e.g. C-Aster reference U2.02.01-A, page 27/50).
Stresses on the clamped area
Here the main procedure is as follows:
- Calculate the effective stresses at the nodes in a RESU file by adding the field (champ) in the command
- result=CALC_NO(...OPTION=(...,'EQUI_NOEU_SIGM',),);
- create a field sigmar of effective stresses at the nodes, defined by a result and a field name:
- sigmar=CREA_CHAMP(...);
- retrieve the table data from the clamped area 'npf1'
- TBsg=POST_RELEVE_T(...);
- and print the table to a file
- IMPR_TABLE(...);
Again, in more detail
result=CALC_NO(reuse =result,
RESULTAT=result,
OPTION=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM','FORC_NODA','REAC_NODA',),);
...
sigmar=CREA_CHAMP(TYPE_CHAM='NOEU_SIEF_R',
OPERATION='EXTR',
RESULTAT=result,
NOM_CHAM='EQUI_NOEU_SIGM',);
TBsig=POST_RELEVE_T(ACTION=(_F(OPERATION='EXTRACTION',
INTITULE='Principal stress',
CHAM_GD=sigmar,
TOUT='OUI',
GROUP_NO='npf1',
TOUT_CMP='OUI',),),
TITRE='Principal stress',);
IMPR_TABLE(TABLE=TBsig,
FORMAT='TABLEAU',
UNITE=26,
SEPARATEUR=' ,',
TITRE='Effective stresses:',);
The first part of the file table.txt on unit 26 contains the following information:
# #-------------------------------------------------------------------------- # #Effective stresses: #Principal stress ,INTITULE ,NOEUD ,CHAM_GD ,ABSC_CURV ,COOR_X ,COOR_Y ,COOR_Z ,VMIS ,TRESCA ,PRIN_1 ,PRIN_2 ,PRIN_3 ,VMIS_SG ,TRSIG ,Principal stress ,N5 ,sigmar , 0.00000E+00 , 0.00000E+00 , 0.00000E+00 , 0.00000E+00 , 5.67306E+07 , 6.63862E+07 ,-3.23391E+07 , 4.64013E+06 , 3.40471E+07 , 5.67306E+07 , 0.00000E+00
....
Input files for creating tables
Here are the input files that have been used:
- python script file for geometry and mesh (change med path to your own needs)
- quad2tb command file and
- solid2t astk file (change base path to your own needs)
- >>> Media:kw_solidplate.zip <<<< *
An up to date version for plotting displacements, stresses etc for version C-A.11.X is available here: [[1]]
-- May 2009 Kees Wouters