Contrib:KeesWouters/beam/macropoutre
back to my main page:
Contrib:KeesWouters
Back to: Use of beam elements
Contrib:KeesWouters/beam
Contents
Software compatibility
march 2011 - SalomeMeca 2010 (Code Aster 10.2) - Ubuntu Meerkat 10.10 64bits.
Using the macro MACR_CARA_POUTRE to define cross section quanties of a beam
This is just another simple example of the use of beams for static calculations. The main focus is on varying obtaining the cross section quantities of the beam by using the macro MACR_CARA_POUTRE. Based on a 2D mesh of the cross section of the beam, most of the required quantities for beam analysis are derived. Here (Contrib:KeesWouters/beam/orientation) an equivalent analysis has been carried out based on a rectangular beam cross section. Here we use an L shaped cross section. Length of the beam is 1.00 [m].
Geometry, mesh, material properties and loads
We need to define two meshes now: one for the cross section of the beam and one for the configuration of the beams.
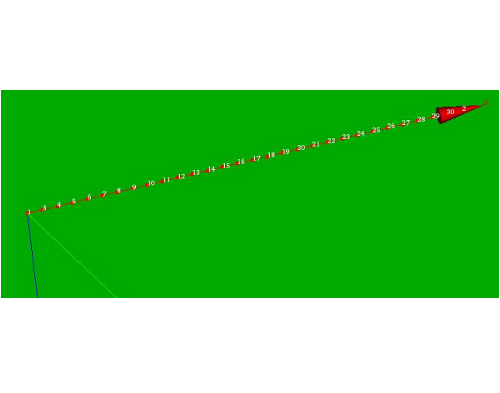
The configuration of the beams: this mesh consists of about thirty beam elements distributed along the x axis.
Note that this has the curious effect that the coordinates of the nodes are defined by a single coordinate. A mesh along the y axis yields a 2D coordinate (x equal to zero). No prices for further guessing.
I decided to read the configuration mesh from unit 20, defined by ASTK:
#Read MED mesh file
BeamMesh=LIRE_MAILLAGE(UNITE=20,
FORMAT='MED',
NOM_MED='Mbeam1',
INFO_MED=2,
INFO=2,);
In the picture below the configuration mesh is shown.
The boundary conditions are: fully clamped at x = 0, free at the opposite end. The load consist of a shear force of 1 [N] in y direction at the end node:
#Define boundary conditions
BndCnd=AFFE_CHAR_MECA(MODELE=BeamMod,
DDL_IMPO=(_F(GROUP_NO='P1',DX=0.0, DY=0.0, DZ=0.0,
DRX=0.0,DRY=0.0,DRZ=0.0,),),
FORCE_NODALE=_F(GROUP_NO='P2',FX=0.0,FY=1.0,FZ=0.0),);
The cross section of the L shaped beam is read from unit 21, also defined by ASTK:
XL=LIRE_MAILLAGE(UNITE=21,
FORMAT='MED',
NOM_MED='AMesh',
INFO_MED=2,
INFO=2,);
Remark:
- the coordinate system is oxy for the definition of the cross section. The local coordinate system of a beam is: x axis equal to the axial axis of the beam and the y and z axes are defined by VECTEUR.
Using the macro MACR_CARA_POUTRE
As seen previously, the cross section of the L shaped beam is read from unit 21:
XL=LIRE_MAILLAGE(UNITE=21,
FORMAT='MED',
NOM_MED='AMesh',
INFO_MED=2,
INFO=2,);
The result structure XL is used by the macro MACR_CARA_POUTRE to retrieve the cross section quantities of it:
Bsection=MACR_CARA_POUTRE(MAILLAGE=XL,
INFO=2,
ORIG_INER=(0.0,0.0),);
The result Bsection is an Aster (table Bsection:<table_sdaster(7f166f039810,'Bsection')> with the geometrical quantities of the cross section.
The table can be written to a file to be examined:
IMPR_TABLE(TABLE=Bsection,
FORMAT='TABLEAU',
UNITE=26,
SEPARATEUR=' * ',
TITRE='xsection of L-beam');
The result:
# # -------------------------------------------------------------------------# #xsection of L-beam #ASTER 10.02.00 CONCEPT Bsection CALCULE LE 26/03/2011 A 15:57:43 DE TYPE #TABLE_SDASTER * LIEU * ENTITE * AIRE_M * CDG_X_M * CDG_Y_M * IX_G_M * IY_G_M * IXY_G_M * Y_MAX * Z_MAX * Y_MIN * Z_MIN * R_MAX * AIRE * CDG_X * CDG_Y * IX_G * IY_G * IXY_G * IY_PRIN_G * IZ_PRIN_G * ALPHA * X_P * Y_P * IX_P * IY_P * IXY_P * IXR2 * IYR2 * IYR2_PRIN_G * IZR2_PRIN_G * IXR2_P * IYR2_P * MAILLAGE
* .... list of Nones (with index 1, next usefull quantities have index 2)
* .9000014 * .9000014 * TOUT * 1.54334E-03 * 1.14339E-02 * 3.95862E-02 * 1.53931E-06 * 2.14464E-07 * -2.96934E-07 * 6.14691E-02 * 1.94603E-02 * -4.67767E-02 * -3.03799E-02 * 6.14862E-02 * 1.54334E-03 * 1.14339E-02 * 3.95862E-02 * 1.53931E-06 * 2.14464E-07 * -2.96934E-07 * 1.50958E-07 * 1.60282E-06 * 1.02072E+02 * 0.00000E+00 * 0.00000E+00 * 3.95783E-06 * 4.16232E-07 * 4.01622E-07 * 1.10571E-08 * 6.24183E-09 * -8.41633E-09 * 9.50713E-09 * 2.99290E-07 * 3.76498E-08 * -
Now suppose you need the area of the cross section AIRE/AIRE_M. This is the third entry (and equal to entry 14 AIRE) of the table. The numerical value is 1.54334E-03 [mm2].
Other interesting quantities are:
- CDG_X_M and CDG_X_M:
- centre of gravity CoG/CDG in x and y direction
- Y_MIN/MAX and Z_MIN/Max:
- minimum and maximum distance from CDG in the main coordinate system 0YZ. The origin coincides with CoG/CDG and is rotated by alpha
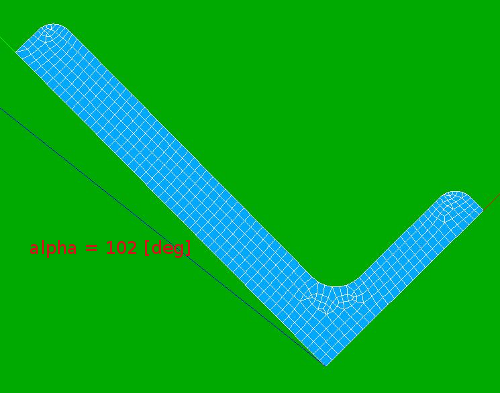
- ALPHA:
- rotation (in [deg]) from global x axis of the mesh to local Y axis of the main coordinate system. In this case alpha = 102 [deg], see also second picture.
- IY_PRIN_G and IZ_PRIN_G:
- Second moment of inertia
For normal static analysis we only need the torsion stiffness CT of the beam. This is not provided by the table.
Using the results inside the command file - I
Having these geometrical quantities print in to a file is nice, having directly access by a Python command is much nicer. You can eg define:
alpha = Bsection['ALPHA', 2] = 1.02072E+02 Iyy = Bsection['IY_PRIN_G', 2] = 1.50958E-07 Izz = Bsection['IZ_PRIN_G', 2] = 1.60282E-06 Area = Bsection['AIRE_M', 2] = 1.54334E-03 CoGX = Bsection['CDG_X', 2] = 1.14339E-02 CoGY = Bsection['CDG_Y', 2] = 3.95862E-02 IyR20 = Bsection['IYR2_PRIN_G',2] =-8.41633E-09 IzR20 = Bsection['IZR2_PRIN_G',2] = 9.50713E-09
print 'alpha0: etc: ',alpha,Iyy,Izz,Area,CoGx,CoGy,IxR20,IyR20
A few remarks:
- index 2 is used because the first index is normally filled with None
- depending on the quantity, the reference coordinate system maybe: [O,X,Y][CoG,X,Y] and [CoG,Yp,Zp]. You need to interpreted the results accordingly.
- the first index is the name also found in the table output
- a number of values is None. For example the torsion stiffness 'CT' is None and thus has not been computed by the macro.
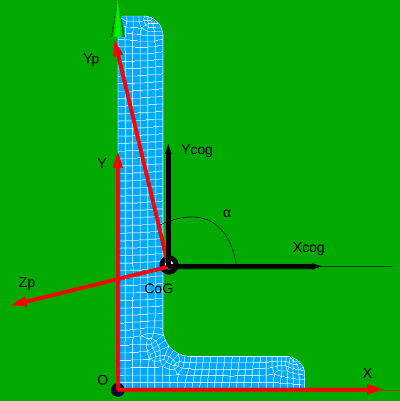
- the values IY_PRIN_G and IZ_PRIN_G are computed with respect to the axes [CoG, Yp, Yz]. The coordinates of CoG are CoGX and CoGY (wrt OXY) and the angle alpha = 102 deg is measured between the axis Xcog of [CoG, Xcog, Ycog] and the axis Yp of [CoG, Yp, Zp], see the figure below.
Using the results inside the command file - II
It is also possible to define a Python variable that extracts the data from the Bsection table.
BSvar = Bsection.EXTR_TABLE() BSvalues = BSvar.values()
- the following types are obtained from:
- print Bsection....................<table_sdaster(7ff0d0bc37d0,'Bsection')>
- print type(BSvalues)............<type 'dict'>
- print type(BSvar)................<class 'Utilitai.Table.Table'>
- print type(BSvar.values).......<type 'instancemethod'>
- print BSvalues['IYR2'][0]......None
- print BSvalues['IYR2'][1]......6.24183205019e-09
Here eg we can extract the following data from BSvalues. BSvalues is a Python dictionary:
Jx = BSvalues['CT'][1] Axy = BSvalues['AIRE'][1] alpha= BSvalues['ALPHA'][1] ## angle of main principle axes CoGx = BSvalues['CDG_X'][1] CoGy = BSvalues['CDG_Y'][1] Iyy = BSvalues['IY_PRIN_G'][1] Izz = BSvalues['IZ_PRIN_G'][1]
Again a remark:
- Note the the last index of BSvalues['AY'][1] is now 1 because Python counts from zero.
Unfortunately the torsion stiffness Jx = CT is not defined here either. The result of print BSvalues:
| output data | MACR_CARA_POUTRE | ||||
|---|---|---|---|---|---|
|
property |
value |
property |
value |
property |
value |
'IYR2' 'EZ' 'IXY_G' 'IY_PRIN_G' 'Z_MIN' 'ENTITE' 'X_P' 'IXY_P' 'JG' 'IZR2_PRIN_G' 'IYR2_P' 'Y_MAX' 'Z_MAX' 'MAILLAGE' |
6.2418320501942666e-09 None -2.9693380576535402e-07 1.5095771271938019e-07 -0.030379887052565866 'TOUT ' 0.0 4.0162157016377599e-07 None 9.5071319311016695e-09 3.7649841463497238e-08 0.06146905080820729 0.019460314808255372 None |
'IYR2_PRIN_G' 'IXR2_P' 'IY_G_M' 'IX_G_M' 'IX_G' 'Y_MIN' 'IY_G' 'IXY_G_M' 'KZ' 'CT' 'CDG_Y_M' 'EY' 'IX_P' 'LIEU' 'AY' |
-8.4163339897006481e-09 2.9929035191926414e-07 2.1446447924954742e-07 1.5393087471625248e-06 1.5393087471625248e-06 -0.046776669698839826 2.1446447924954742e-07 -2.9693380576535402e-07 None None 0.039586221722664502 None 3.9578309685899442e-06 '.9000014' None |
'CDG_X_M' 'AZ' 'PCTY' 'IY_P' 'CDG_X' 'CDG_Y' 'PCTX' 'AIRE' 'IXR2' 'Y_P' 'IZ_PRIN_G' 'R_MAX' 'ALPHA' 'KY' 'AIRE_M' |
0.011433911068540359 None None 4.1623215742762136e-07 0.011433911068540359 0.039586221722664502 None 0.0015433412939497826'IZ_PRIN_G' 1.1057113910905097e-08 0.0 1.6028155136926921e-06 0.061486249910580375 102.07226511894622 None 0.0015433412939497826 |
Note that 'IZ_PRIN_G' is about 10 times larger than 'IY_PRIN_G', in agreement with the larger dimension of the L-beam in the Yp direction.
Orientation of the beam
For a rectangular cross section of a beam, the characteristics are defined by:
RBeam=AFFE_CARA_ELEM(MODELE=BeamMod,
POUTRE=(_F(GROUP_MA='beam1',
SECTION='RECTANGLE',
CARA=('HY','HZ','EP',),
VALE=(0.0200,0.0100,0.0025,),),),
ORIENTATION=(_F(GROUP_MA='beam1',
CARA='VECT_Y',
VALE=(0.0,0.0,1.0,),),),)
This command is described here: [[1]].
For a general shape, using the macro MACR_ACC_POUTRE and its result, this command can be used as follows:
Ry = math.cos(alpha/math.pi)
Rz = math.sin(alpha/math.pi)
GBeam=AFFE_CARA_ELEM(MODELE=BeamMod,
POUTRE=_F(GROUP_MA='beam1',SECTION='GENERALE',
CARA= ( 'A', 'IY','IZ','AY','AZ','JX'),
VALE= ( Axy ,Iyy, Izz, Ay, Az, Jx),),
ORIENTATION=(_F(GROUP_MA='beam1',
CARA='VECT_Y',
VALE=(0,Ry,Rz),),),);
In POUTRE, the common parameters A (area), IY, IZ, AY, AZ (maximum distance of fibre to CoG in z direction) and JX (torsion stiffness) need to be given. The fields in CARA and VALE are linked, ie same order is applied. If needed more quantities can be added. In ORIENTATION the VECT_Y defines the local y direction. The projection of the vector VALE=(Rx,Ry,Rz) on the local x axis defines the local y axis of the beam. In this case the local y axis is equal to the axis Yp of the principal coordinate system [CoG,Yp,Yz].
Applying material and boundary conditions
The commands for defining material properties and boundary conditions are:
#Assign material to mesh BeamMat=AFFE_MATERIAU(MAILLAGE=BeamMesh,AFFE=_F(TOUT='OUI',MATER=Steel,),);
#Define boundary conditions
BndCnd=AFFE_CHAR_MECA(MODELE=BeamMod,
DDL_IMPO=(
_F(GROUP_NO='P1',DX=0.0, DY=0.0, DZ=0.0,
DRX=0.0,DRY=0.0,DRZ=0.0,),),
FORCE_NODALE=
_F(GROUP_NO='P2',FX=0.0,FY=1.0,FZ=0.0),);
Start and post process the analysis
The mechanical calculation can be started by:
#Execute analysis
solB=MECA_STATIQUE(MODELE=BeamMod,
CHAM_MATER=BeamMat,
CARA_ELEM=GBeam,
EXCIT=_F(CHARGE=BndCnd,),);
The results at the nodes:
solB=CALC_NO(reuse =solB,
RESULTAT=solB,
OPTION='FORC_NODA',
MODELE=BeamMod,
TOUT='OUI',);
The results at the elements:
solB=CALC_ELEM(reuse =solB,
MODELE=BeamMod,
RESULTAT=solB,
TOUT='OUI',
OPTION='SIEF_ELNO_ELGA',);
Printing the results to files:
#Print to results file to a text file
IMPR_RESU(MODELE=BeamMod,
FORMAT='RESULTAT',
UNITE=8,
RESU=_F(MAILLAGE=BeamMesh,
RESULTAT=solB,
TOUT_CHAM='OUI',
TOUT_PARA='OUI',
TOUT_CMP='OUI',
TOUT='OUI',
FORMAT_R='1PE12.5',),);
#Export to MED file
IMPR_RESU(MODELE=BeamMod,
FORMAT='MED',
UNITE=80,
RESU=_F(MAILLAGE=BeamMesh,
RESULTAT=solB,
INFO_MAILLAGE='OUI',
TOUT_CMP='OUI',
TOUT='OUI',),);
# print displacements of selective nodes - first define table
TB_disp=POST_RELEVE_T(ACTION=(_F(OPERATION='EXTRACTION',
INTITULE='displacements dz',
RESULTAT=solB,
NOM_CHAM='DEPL',
TOUT_ORDRE='OUI',
NOEUD=('N1','N2','N10','N20'),
NOM_CMP=('DX','DY','DZ',),),),);
# and print to a text file:
IMPR_TABLE(TABLE=TB_disp,
FORMAT='TABLEAU',
UNITE=26,
SEPARATEUR=' * ',
TITRE='reaction forces at nodes on group Nsupport');
FIN(FORMAT_HDF='OUI',);
Numerical results
For a bending force of 1 [N] in y direction at the end node of the beam, the displacements in x, y and z direction are as follows:
Xcoord Ydisp * Zdisp Nclamp 0.00000E+00 3.23117E-25 * -7.66769E-25 Nforce 1.00000E+00 9.99732E-06 * 2.15908E-06 N2 3.80826E-01 1.89877E-06 * 4.10069E-07 N10 8.57521E-01 7.87516E-06 * 1.70077E-06
Euler verification for Nforce:
Displacements in the principle axes of the beam: [OYpZp]:
dyp = -Fy*cos(alpha)*L^3/(3*E*Izz) --> -2.0712e-07 [m] dzp = -Fy*sin(alpha)*L^3/(3*E*Iyy) --> -1.0282e-05 [m]
Transform back to global [OXYZ]:
dy = cos(alpha)*dyp + sin(alpha)*dzp = dz = -sin(alpha)*dyp + cos(alpha)*dzp =
For the case alpha = 90 [deg], ie. VECT_Y = (0,0,1):
Fy=1, Fz=0: dy = Fy*L^3/(3*E*Iyy) --> 1.051e-05 [m] Fy=0, Fz=1: dz = Fz*L^3/(3*E*Izz) --> 9.903e-07 [m]