Date: 21 février 2007
| Version | Date | Modifications | Auteur(s) |
|---|---|---|---|
| 01 | 28/01/2007 | Création | PC |
Mots clefs : thermomécanique, projection, maillage tétra, maillage héxa, MECA_STATIQUE.
Ce document se voulant interactif, le signalement de toute erreur est le bienvenu ![]() il en va de même pour les améliorations.
il en va de même pour les améliorations.
Le lecteur est invité à lire le tutorial 1 (CAELINUX_post-traitement.pdf) traitant spécifiquement du post-traitement (graphique) des résultats ; il y trouvera quelques façons de visualiser les résultats (déplacements, champs de contraintes, courbes, etc. ...). De cette façon, les différents tutoriaux se concentreront sur le thème de la note.
L'autre particularité du document réside dans l'utilisation de 2 maillages notablement différents :
Les calculs ont été réalisés sous Code Aster
![]() V8.3.
V8.3.
La figure 2 présente le maillage "thermique".
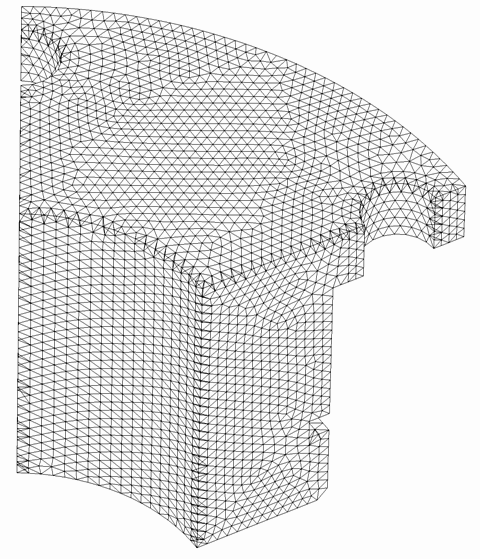
|
Il est en effet dommage de relancer tout un calcul (particulièrement si celui-ci est long) pour une problématique de post-traitement (recherche d'un instant particulier, calcul d'une grandeur supplémentaire ![]() ou tout simplement une erreur de post-traitement).
ou tout simplement une erreur de post-traitement).
Etape 1 : calcul thermique
F mess /symetrie_cyclique_TH.mess R 6 F erre /symetrie_cyclique_TH.erre R 9 R base /base_TH R 0 F unv /symetrie_cyclique_tetra.unv D 19 F unv /symetrie_cyclique_hexa.unv D 21 F comm /symetrie_cyclique_TH.comm D 1
Etape 2 : Post-traitement des résultats thermiques - sous Gibi ici
F mess /symetrie_cyclique_TH_post.mess R 6 F erre /symetrie_cyclique_TH_post.erre R 9 R base /base_TH D 0 F comm /symetrie_cyclique_TH_post.comm D 1 F cast /symetrie_cyclique_TH.cast R 50
Etape 3 : calcul mécanique
F mess /symetrie_cyclique_MEC.mess R 6 F erre /symetrie_cyclique_MEC.erre R 9 R base /base_TH D 0 R base /base_MECA R 0 F comm /symetrie_cyclique_MEC.comm D 1
Etape 4 : Post-traitement des résultats mécaniques - sous Gibi ici
F comm /symetrie_cyclique_MEC_post.comm D 1 R base /base_MECA D 0 F mess /symetrie_cyclique_MEC_post.mess R 6 F resu /symetrie_cyclique_MEC_post.resu R 8 F erre /symetrie_cyclique_MEC_post.erre R 9 F cast /symetrie_cyclique_MEC_post.cast R 50
PRE_IDEAS(UNITE_IDEAS=19,
UNITE_MAILLAGE=20,);
MAIL_TH=LIRE_MAILLAGE(UNITE=20,);
#Lecture du maillage mécanique
PRE_IDEAS(UNITE_IDEAS=21,
UNITE_MAILLAGE=22,);
MAIL_MEC=LIRE_MAILLAGE(UNITE=22,);
#Definition & affectation des modèles
MOD_TH=AFFE_MODELE(MAILLAGE=MAIL_TH,
AFFE=_F(TOUT='OUI',
PHENOMENE='THERMIQUE',
MODELISATION='3D',),);
MOD_MEC=AFFE_MODELE(MAILLAGE=MAIL_MEC,
AFFE=_F(TOUT='OUI',
PHENOMENE='MECANIQUE',
MODELISATION='3D_SI',),);
Nous définissons les caractéristiques thermiques du matériau, à savoir la conductivité thermique ![]() =14.9 mW/mm-
=14.9 mW/mm-![]() C et la chaleur volumique
C et la chaleur volumique
![]() =3.76 mJ/mm
=3.76 mJ/mm![]() .
.
BIDON_TH=DEFI_MATERIAU(THER=_F(LAMBDA=14.9,
RHO_CP=3.76,),);
MAT_TH=AFFE_MATERIAU(MAILLAGE=MAIL_TH,
AFFE=_F(TOUT='OUI',
MATER=BIDON_TH,),);
A l'instar du calcul mécanique, il est possible d'exploiter la symétrie cyclique de la pièce en imposant des conditions adiabatiques aux 2 plans de symétrie ; cela se traduit par un flux imposé nul (![]() ).
).
Rappelons que les températures s'appliquent aux noeuds (le groupe de mailles T_IMPO est transformé en groupe de noeuds avec DEFI_GROUP), les flux et les échanges convectifs sur les faces (cf. figure 4).
MAIL_TH=DEFI_GROUP(reuse =MAIL_TH,
MAILLAGE=MAIL_TH,
CREA_GROUP_NO=_F(GROUP_MA='T_IMPO',),);
CL_TH=AFFE_CHAR_THER(MODELE=MOD_TH,
TEMP_IMPO=_F(GROUP_NO='T_IMPO',
TEMP=200,),
FLUX_REP=_F(GROUP_MA='ADIAB',
FLUN=0.0,),
ECHANGE=_F(GROUP_MA='CONV',
COEF_H=0.5,
TEMP_EXT=20,),);
RESOL_TH=THER_LINEAIRE(MODELE=MOD_TH,
CHAM_MATER=MAT_TH,
EXCIT=_F(CHARGE=CL_TH,),
TEMP_INIT=_F(STATIONNAIRE='OUI',),);
POURSUITE();
RESOL_TH=CALC_ELEM(reuse =RESOL_TH,
RESULTAT=RESOL_TH,
OPTION='FLUX_ELNO_TEMP',);
IMPR_RESU(FORMAT='CASTEM',
UNITE=50,
RESU=_F(MAILLAGE=MAIL_TH,
RESULTAT=RESOL_TH,
NOM_CHAM=('TEMP','FLUX_ELNO_TEMP',),),);
FIN();
A noter que le maillage DOIT ABSOLUMENT être imprimé dans le fichier résultat (cf. MAILLAGE=MAIL_TH,).
Les figures 5 et 6 présentent le résultat graphique.
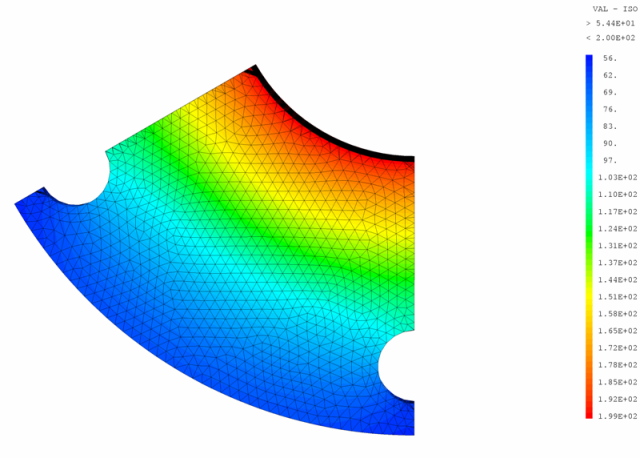
|
PROJ_TH=PROJ_CHAMP(RESULTAT=RESOL_TH,
MODELE_1=MOD_TH,
MODELE_2=MOD_MEC,
VIS_A_VIS=_F(TOUT_1='OUI',
TOUT_2='OUI',
CAS_FIGURE='3D',),);
Le reste de la mise en données est assez classique.
| Température | Module d'YOUNG E | Coefficient de | Coefficient de POISSON |
|---|---|---|---|
| dilatation thermique | |||
| [ |
[MPa] | [/ |
[adimensionel] |
| 20 | 193000 | ref. | 0.3 |
| 100 | 186000 |
|
0.3 |
| 200 | 178000 |
|
0.3 |
| 300 | 170000 |
|
0.3 |
Ces propriétés sont affectées à l'ensemble du maillage.
ALPHA_T=DEFI_FONCTION(NOM_PARA='TEMP',
VALE=
(100,16.4E-6,200,17E-6,300,17.5E-6,),
PROL_DROITE='CONSTANT',
PROL_GAUCHE='CONSTANT',);
YOUNG_T=DEFI_FONCTION(NOM_PARA='TEMP',
VALE=
(20,193000,100,186000,200,178000,300,170000,),
PROL_DROITE='CONSTANT',
PROL_GAUCHE='CONSTANT',);
POISSON=DEFI_CONSTANTE(VALE=0.3,);
SS304L=DEFI_MATERIAU(ELAS_FO=_F(E=YOUNG_T,
NU=POISSON,
RHO=8.47e-009,
TEMP_DEF_ALPHA=20.0,
ALPHA=ALPHA_T,),);
MATERIAU=AFFE_MATERIAU(MAILLAGE=MAIL_MEC,
AFFE=_F(TOUT='OUI',
MATER=SS304L,
TEMP_REF=20.0,),);
La définition du repère local se fait au travers de LIAISON_OBLIQUE dans AFFE_CHAR_MECA (nous retrouvons les 60![]() dans la définition de l'angle nautique3).
dans la définition de l'angle nautique3).
Nous avons choisi d'utiliser ici des groupes de mailles (que nous transformons en groupe de noeuds avec CREA_GROUP_NO dans DEFI_GROUP).
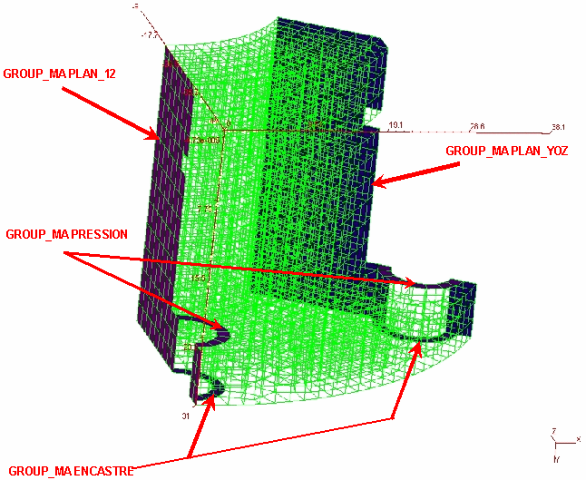
|
Contrairement aux éléments de coque ou de poutre (6 DDL), les éléments volumiques sont définis par 3 DDL (les 3 translations - comme pour les membranes et les barres) qu'il convient de bloquer sous peine d'avoir des pivots nuls (signe que le système est hypostatique et donc insoluble).
Le système reste isostatique en bloquant les noeuds des groupes (cf. 7) :
NOTA :
Suite aux remarques précédentes, des opérations booléennes sont opérées de façon à retirer les noeuds communs aux 2 groupes de ENCASTRE selon le schéma :
Ce qui donne :
MAIL=DEFI_GROUP(reuse =MAIL,
MAILLAGE=MAIL,
CREA_GROUP_NO=(_F(GROUP_MA='ENCASTRE',),
_F(GROUP_MA='PLAN_12',),
_F(GROUP_MA='PLAN_YOZ',),),);
MAIL=DEFI_GROUP(reuse =MAIL,
MAILLAGE=MAIL,
CREA_GROUP_NO=(_F(INTERSEC=('ENCASTRE','PLAN_12',),
NOM='ENCAS_LO',),
_F(DIFFE=('ENCASTRE','ENCAS_LO',),
NOM='ENCASTRG',),),);
Le blocage des CL devient alors :
CL=AFFE_CHAR_MECA(MODELE=MOD_MEC,
DDL_IMPO=(_F(GROUP_NO='ENCASTRG',
DY=0,),
_F(GROUP_NO='PLAN_YOZ',
DX=0,),),
LIAISON_OBLIQUE=(_F(GROUP_NO='PLAN_12',
ANGL_NAUT=(0,-60.0,0,),
DX=0,),
_F(GROUP_NO='ENCAS_LO',
ANGL_NAUT=(0,-60,0,),
DY=0,),),);
CHARGMNT=AFFE_CHAR_MECA(MODELE=MOD_MEC,
TEMP_CALCULEE=PROJ_TH,
PESANTEUR=(0,-1,0,981000,),
PRES_REP=_F(GROUP_MA='PRESSION',
PRES=172.81,),);
NOTA : Pour calculer les dilatations de la pièce, il est nécessaire d'indiquer à Code Aster
![]() l'existence d'un champ thermique grâce à TEMP_CALCULEE dans AFFE_CHAR_MECA.
l'existence d'un champ thermique grâce à TEMP_CALCULEE dans AFFE_CHAR_MECA.
Pour le chargement, nous cherchons à modéliser un pseudo-serrage5 sous la forme d'une pression (correspondant à une vis ChC de M6 serrée à 10 NM). Nous supposerons que la pièce se dilate librement sous la tête de vis. Pour le fun, nous supposons une gravité de 100G.
Rappelons que toute pression s'exerce en sens inverse de la normale (sortante) des faces (cette dernière est définie par la topologie des éléments) ; il est préférable de demander à Code Aster
![]() de réorienter les normales des groupes de mailles utilisés (au pire il ne réoriente aucune maille ; au mieux il évite une erreur) :
de réorienter les normales des groupes de mailles utilisés (au pire il ne réoriente aucune maille ; au mieux il évite une erreur) :
MAIL=MODI_MAILLAGE(reuse =MAIL,
MAILLAGE=MAIL,
ORIE_PEAU_3D=_F(GROUP_MA='PRESSION',),
MODELE=MODELE,);
CHARGMNT=AFFE_CHAR_MECA(MODELE=MODELE,
PESANTEUR=(0,-1,0,981000,),
PRES_REP=_F(GROUP_MA='PRESSION',
PRES=172.81,),);
RESOL_ME=MECA_STATIQUE(MODELE=MOD_MEC,
CHAM_MATER=MATERIAU,
EXCIT=(_F(CHARGE=CHARGMNT,),
_F(CHARGE=CL,),),);
POURSUITE();
RESOL=CALC_ELEM(reuse =RESOL,
RESULTAT=RESOL,
OPTION=('SIGM_ELNO_DEPL','EQUI_ELNO_SIGM',),);
IMPR_RESU(FORMAT='CASTEM',
UNITE=51,
RESU=_F(MAILLAGE=MAIL,
RESULTAT=RESOL,
NOM_CHAM=('SIGM_ELNO_DEPL','EQUI_ELNO_SIGM','DEPL',),),);
FIN();
A noter que le maillage DOIT ABSOLUMENT être imprimé dans le fichier résultat (cf. MAILLAGE=MAIL_MEC,).
Les figures 9 et 10 présentent les isovaleurs de déplacements ; les 2 suivantes (fig 12 & 13) sont intéressantes parce qu'elles visualisent les vecteurs déplacements.
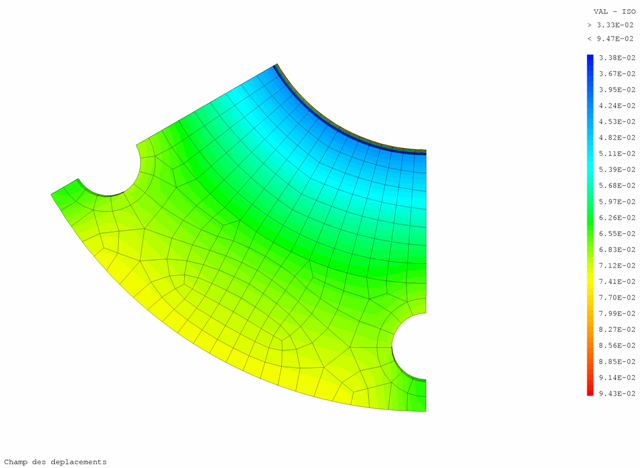
|
Une fonctionnalité intéressante : il est possible de superposer le maillage déformé sur le maillage initial (cf. figure 11).
Les cartographies des contraintes sont visibles aux figures 14 et 15.
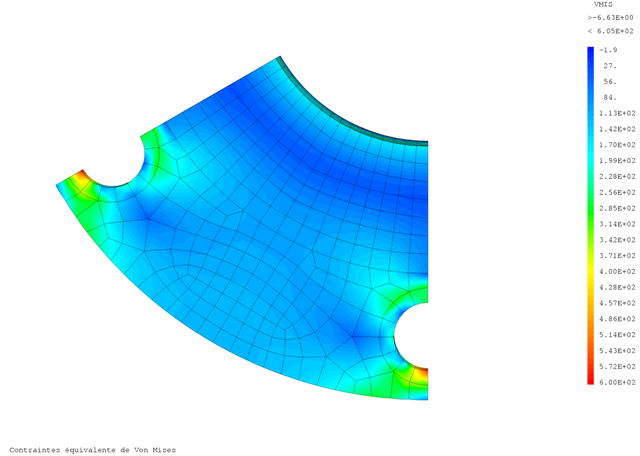
|
De même, il est possible de visualiser les champs de contraintes sur le maillage déformée (cf. figure 16.
DEBUT();
#Lecture des maillages :
#Lecture maillage thermique
PRE_IDEAS(UNITE_IDEAS=19,
UNITE_MAILLAGE=20,);
MAIL_TH=LIRE_MAILLAGE(UNITE=20,);
#Lecture du maillage mécanique
PRE_IDEAS(UNITE_IDEAS=21,
UNITE_MAILLAGE=22,);
MAIL_MEC=LIRE_MAILLAGE(UNITE=22,);
#Definition & affectation des modèles
MOD_TH=AFFE_MODELE(MAILLAGE=MAIL_TH,
AFFE=_F(TOUT='OUI',
PHENOMENE='THERMIQUE',
MODELISATION='3D',),);
MOD_MEC=AFFE_MODELE(MAILLAGE=MAIL_MEC,
AFFE=_F(TOUT='OUI',
PHENOMENE='MECANIQUE',
MODELISATION='3D_SI',),);
BIDON_TH=DEFI_MATERIAU(THER=_F(LAMBDA=14.9,
RHO_CP=3.76,),);
MAT_TH=AFFE_MATERIAU(MAILLAGE=MAIL_TH,
AFFE=_F(TOUT='OUI',
MATER=BIDON_TH,),);
#Défintion du chargement thermique :
#- GROUP_MA : ADIAB => flux nul (symétrie)
#- GROUP_MA : CONV => convection forcée
#- GROUP_MA : T_IMPO => T imposée
MAIL_TH=DEFI_GROUP(reuse =MAIL_TH,
MAILLAGE=MAIL_TH,
CREA_GROUP_NO=_F(GROUP_MA='T_IMPO',),);
CL_TH=AFFE_CHAR_THER(MODELE=MOD_TH,
TEMP_IMPO=_F(GROUP_NO='T_IMPO',
TEMP=200,),
FLUX_REP=_F(GROUP_MA='ADIAB',
FLUN=0.0,),
ECHANGE=_F(GROUP_MA='CONV',
COEF_H=0.5,
TEMP_EXT=20,),);
#Solveur thermique
RESOL_TH=THER_LINEAIRE(MODELE=MOD_TH,
CHAM_MATER=MAT_TH,
EXCIT=_F(CHARGE=CL_TH,),
TEMP_INIT=_F(STATIONNAIRE='OUI',),);
FIN();
POURSUITE();
RESOL_TH=CALC_ELEM(reuse =RESOL_TH,
RESULTAT=RESOL_TH,
OPTION='FLUX_ELNO_TEMP',);
IMPR_RESU(FORMAT='CASTEM',
UNITE=50,
RESU=_F(MAILLAGE=MAIL_TH,
RESULTAT=RESOL_TH,
NOM_CHAM=('TEMP','FLUX_ELNO_TEMP',),),);
RESOL_TH=CALC_NO(reuse =RESOL_TH,
RESULTAT=RESOL_TH,
OPTION='FLUX_NOEU_TEMP',);
IMPR_RESU(FORMAT='GMSH',
UNITE=51,
RESU=_F(RESULTAT=RESOL_TH,
NOM_CHAM='TEMP',),);
FIN();
POURSUITE();
#Projection du champ thermique du maillage thermique (tétra linéaire)
# sur le maillage mécanique (hexa quadratique)
PROJ_TH=PROJ_CHAMP(RESULTAT=RESOL_TH,
MODELE_1=MOD_TH,
MODELE_2=MOD_MEC,
VIS_A_VIS=_F(TOUT_1='OUI',
TOUT_2='OUI',
CAS_FIGURE='3D',),);
#Préparation du modèle mécanique :
#- réorientation des normales pour l'application d'une pression
MAIL_MEC=MODI_MAILLAGE(reuse =MAIL_MEC,
MAILLAGE=MAIL_MEC,
ORIE_PEAU_3D=_F(GROUP_MA='PRESSION',),
MODELE=MOD_MEC,);
#- Création des groupes de noeuds pour les CL
MAIL_MEC=DEFI_GROUP(reuse =MAIL_MEC,
MAILLAGE=MAIL_MEC,
CREA_GROUP_NO=(_F(GROUP_MA='ENCASTRE',),
_F(GROUP_MA='PLAN_12',),
_F(GROUP_MA='PLAN_YOZ',),),);
MAIL_MEC=DEFI_GROUP(reuse =MAIL_MEC,
MAILLAGE=MAIL_MEC,
CREA_GROUP_NO=(_F(INTERSEC=('ENCASTRE','PLAN_12',),
NOM='ENCAS_LO',),
_F(DIFFE=('ENCASTRE','ENCAS_LO',),
NOM='ENCASTRG',),),);
#Propriétés des caractéristiques mécaniques du matériaux
ALPHA_T=DEFI_FONCTION(NOM_PARA='TEMP',
VALE=
(100,16.4E-6,200,17E-6,300,17.5E-6,),
PROL_DROITE='CONSTANT',
PROL_GAUCHE='CONSTANT',);
YOUNG_T=DEFI_FONCTION(NOM_PARA='TEMP',
VALE=
(20,193000,100,186000,200,178000,300,170000,),
PROL_DROITE='CONSTANT',
PROL_GAUCHE='CONSTANT',);
POISSON=DEFI_CONSTANTE(VALE=0.3,);
SS304L=DEFI_MATERIAU(ELAS_FO=_F(E=YOUNG_T,
NU=POISSON,
RHO=8.47e-009,
TEMP_DEF_ALPHA=20.0,
ALPHA=ALPHA_T,),);
MATERIAU=AFFE_MATERIAU(MAILLAGE=MAIL_MEC,
AFFE=_F(TOUT='OUI',
MATER=SS304L,
TEMP_REF=20.0,),);
#Définition des conditions aux limites :
#- LIAISON_OBLIQUE => Chargement de repère
CL=AFFE_CHAR_MECA(MODELE=MOD_MEC,
TEMP_CALCULEE=PROJ_TH,
DDL_IMPO=(_F(GROUP_NO='ENCASTRG',
DY=0,),
_F(GROUP_NO='PLAN_YOZ',
DX=0,),),
LIAISON_OBLIQUE=(_F(GROUP_NO='PLAN_12',
ANGL_NAUT=(0,-60.0,0,),
DX=0,),
_F(GROUP_NO='ENCAS_LO',
ANGL_NAUT=(0,-60,0,),
DY=0,),),);
CHARGMNT=AFFE_CHAR_MECA(MODELE=MOD_MEC,
PESANTEUR=(0,-1,0,981000,),
PRES_REP=_F(GROUP_MA='PRESSION',
PRES=172.81,),);
RESOL_ME=MECA_STATIQUE(MODELE=MOD_MEC,
CHAM_MATER=MATERIAU,
EXCIT=(_F(CHARGE=CHARGMNT,),
_F(CHARGE=CL,),),);
FIN();
POURSUITE();
RESOL_ME=CALC_ELEM(reuse =RESOL_ME,
RESULTAT=RESOL_ME,
OPTION=('SIGM_ELNO_DEPL','EQUI_ELNO_SIGM',),);
RESOL_ME=CALC_NO(reuse =RESOL_ME,
RESULTAT=RESOL_ME,
OPTION=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM',),);
IMPR_RESU(FORMAT='CASTEM',
UNITE=50,
RESU=_F(MAILLAGE=MAIL_MEC,
RESULTAT=RESOL_ME,
NOM_CHAM=('DEPL','SIGM_ELNO_DEPL','EQUI_ELNO_SIGM',),),);
IMPR_RESU(FORMAT='GMSH',
UNITE=51,
RESU=_F(RESULTAT=RESOL_ME,
NOM_CHAM='EQUI_NOEU_SIGM',
NOM_CMP='VMIS',),);
IMPR_RESU(FORMAT='GMSH',
UNITE=52,
RESU=_F(RESULTAT=RESOL_ME,
NOM_CHAM='DEPL',),);
Remerciements : L'auteur(s) souhaite(nt) remercier les personnes de la communauté de Code Aster
![]() et de Cast3M
et de Cast3M
![]() qui ont fourni aides et informations précieuses : qu'ils en soient chaleureusement remercier. L'ensemble des notes présentes sur le site ne sont que la continuation de cet esprit "libre" qui vise entre-autres choses partager son savoir et son travail
qui ont fourni aides et informations précieuses : qu'ils en soient chaleureusement remercier. L'ensemble des notes présentes sur le site ne sont que la continuation de cet esprit "libre" qui vise entre-autres choses partager son savoir et son travail ![]()
L'auteur : Paul CARRICO6.
Les commentaires sont à adresser à :
paul.carrico_at_free.fr
| Unités | METRIQUE | METRIQUE | ANGLO-SAXONNE | ANGLO-SAXONNE |
|---|---|---|---|---|
| MKS | mmNS | FPS | IPS | |
| Longueur | m | mm | ft | in |
| Temps | sec | sec | sec | sec |
| Masse | Kg | tonne | slug | lbf-sec |
| Force | N | N | lbf | lbf |
| Température | ||||
| Aire | m |
mm |
ft |
in |
| Volume | m |
mm |
ft |
in |
| Vitesse | m/sec | mm/sec | ft/sec | in/sec |
| Accélération | m/sec |
mm/sec |
ft/sec |
in/sec |
| Angle, rotation | rad | rad | rad | rad |
| Vitesse angulaire | rad/sec |
rad/sec |
rad/sec |
rad/sec |
| Masse volumique | Kg/m |
Tonne/mm |
slug/ft |
lbf-sec |
| Moment, couple | N-m | N-mm | ft-lbf | in-lbf |
| Force linéïque | N/m | N/mm | lbf/ft | lbf/in |
| Force répartie sur une surface | N/m |
N/mm |
lbf/ft |
lbf/in |
| (Contrainte, pression,Module d'Young) | (Pa) | (MPa) | (Psi) | |
| Coefficient de Dilatation thermique | / |
/ |
/ |
/ |
| (/K) | (/K) | (/K) | (/K) | |
| Moment Quadratique d'une poutre |
m |
mm |
ft |
in |
| Moment d'inertie transverse d'une poutre | Kg-m |
tonne-mm |
slug-ft |
lbf-in-sec |
| Energie, Travail, Chaleur | J | mJ | ft-lbf | in-lbf |
| Puissance, taux de transfert thermique | W | mW | ft-lbf/sec | in-lbf/sec |
| Gradient de température | ||||
| Flux thermique | W/m |
mW/mm |
lbf/ft-sec | lbf/in-sec |
| Conductivité thermique | W/m- |
mW/mm- |
lbf/sec- |
lbf/sec- |
| Chaleur spécifique C |
J/Kg- |
mJ/tonne- |
ft-lbf/slug- |
in |
Rappels :
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 CAELINUX_thermomecanique.tex
The translation was initiated by on 2007-02-21