T1phvmn

Tutorial 1 :
Post-traitements des résultats
Utilisation des outils connexes à Code Aster $^{\tiny {\textregistered }}$
Version 1

Date: 21 février 2007

Table des matières

Table des évolutions

Version	Date	Modifications	Auteur(s)
01	28/01/2007	Création	PC

Mots clefs : Post-traitement graphique, GMSH, GIBI $^{\tiny {\textregistered }}$ , SALOME $^{\tiny {\textregistered }}$ , GRACE $^{\tiny {\textregistered }}$ .

Avant propos

J'ai pris le parti de séparer les calculs à proprement parlé des considérations de pré & post-traitement. En effet, nombres d'astuces pourront être partagées par la communauté et il m'apparaît plus simple (et plus pertinent) de modifier un seul et unique document plutôt que de mettre à jours x tutoriaux pour la même idée $\ldots$ et cela évite de rendre les documents indigestes par une abondance de détails sans rapport forcement avec le thème du document.

Enfin, les exemples traités ici reprennent les résultats des tutoriaux présents sur le site de CAELINUX, ces derniers faisant eux-même référence à cette note pour la partie post-traitement.

Introduction

Code aster $^{\tiny {\textregistered }}$ est un solveur c'est-à-dire qu'il ne traite que de la partie calcul. Concrètement cela signifie que le maillage et la visualisation graphique des résultats requièrent l'utilisation d'outils spécifiques (libres ou propriétaires).

Fort heureusement Code Aster $^{\tiny {\textregistered }}$ est livré avec certains d'entre eux que nous nous proposons d'utiliser ici :

GMSH et GIBI $^{\tiny {\textregistered }}$ pour la partie visualisation des isovaleurs,
GRACE $^{\tiny {\textregistered }}$ pour la réalisation de courbes,

Cette liste n'est pas exhaustive ; il est possible d'utiliser d'autres outils comme PARAVIEW $^{\tiny {\textregistered }}$ puisque Code Aster $^{\tiny {\textregistered }}$ exporte les résultats au format ENSIGHT $^{\tiny {\textregistered }}$ , ou CGX.

Nous nous intéresserons également à SALOME $^{\tiny {\textregistered }}$ (pré & post-traitement au format MED), disponible sous licence GPL auquel EDF $^{\tiny {\copyright}}$ participe activement.

Types de résultats exploitables en post-traitement

Le post-traitement graphique des résultats peut se faire :

$\triangleright$: Par élément (valeur moyenne par élément),
$\triangleright$: Par extrapolation aux noeuds,
$\triangleright$: Directement aux points d'intégration,

Post-traitements sous GMSH

GMSH est un outil assez complet et probablement le plus simple à utiliser. Il permet en effet de visualiser champs scalaires (contraintes équivalentes, isovaleurs de déplacements, etc ...) et champs vectoriels ; ils disposent de plugins intéressants (coupes, visualisations de groupes de mailles, etc. ...).

Il est surtout d'une prise en main facile où tout se fait à la souris (translations, rotations, grossissements, réductions, etc. ....).

Il présente néanmoins l'inconvénient de ne pas prendre en compte les éléments du second ordre (SEG3, QUAD8, TETRA10 et HEXA20) ; les développeurs de Code Aster ont contourné le problème en créant un nouveau maillage tel que les noeuds deviennent tous des noeuds sommet. Le principal inconvénient se situe au niveau de la taille des fichiers de post-traitement qui peuvent "`exploser"' pour de gros maillages quadratiques (particulièrement en transitoire ou en non-linéaires si plusieurs pas de temps sont archivés).

NOTA : GMSH est assez intuitif et on ne saurait trop conseiller le lecteur de consacrer un peu de son temps au test des différentes fonctionnalités ; nous traiterons donc uniquement de la façon d'exporter les résultats depuis Code Aster.

Valeurs moyennes aux éléments

Sauf erreur, GMSH ne permet pas ce type d'affichage et il faudra lui préférer un autre outil comme GIBI $^{\tiny {\textregistered }}$ par exemple.

Extrapolation aux noeuds

Mise en données sous EFICAS $^{\tiny {\textregistered }}$

Nous pensons qu'il est plus pertinent de lancer les simulations en 2 temps :

$\triangleright$: Le calcul à proprement parlé,
$\triangleright$: Le post-traitement,

Il est en effet dommage de relancer tout un calcul (particulièrement si celui-ci est long) pour une problématique de post-traitement (recherche d'un instant particulier, calcul d'une grandeur supplémentaire $\ldots$ ou tout simplement pour une erreur de mise en données).

Sous ASTK $^{\tiny {\textregistered }}$ , le fichier est par exemple de la forme :

F comm /symetrie_cyclique_post.comm D 1
R base /base_symetrie_cyclique D 0
F mess /symetrie_cyclique_post.mess R 6
F erre /symetrie_cyclique_post.erre R 9
F resu /symetrie_cyclique_post.resu R 8
F pos /symetrie_cyclique_vmis.pos R 51
F pos /symetrie_cyclique_depl.pos R 52

RAPPEL :

$\triangleright$: Les unités 1,6,9,8 sont spécifiques et correspondent respectivement au .comm, .mess, .erre et .resu $\ldots$ ils sont attribués par ASTK $^{\tiny {\textregistered }}$ et le lecteur n'a pas à les modifier : 51 & 52 correspondent aux unités des fichiers GMSH qui ont été affectées dans le .comm.,
$\triangleright$: Les lettres R et D correspondantes signifient R(esult) & D(ata),
$\triangleright$: Tout à droite les lettres F & R désignent F(ile) & R(epertory).

Par la suite, nous distingueront les calculs linéaires (mécanique & thermiques) des calculs non-linéaires & transitoires.

Calcul thermique linéaires - stationnaire

L'idée est ici de visualiser les champs de températures dans la pièce (champ scalaire). Le fichier de post-traitement sous Code Aster $^{\tiny {\textregistered }}$ est de la forme :

POURSUITE();
RESOL_TH=CALC_ELEM(reuse =RESOL_TH,
                   RESULTAT=RESOL_TH,
                   OPTION='FLUX_ELNO_TEMP',);
                   
RESOL_TH=CALC_NO(reuse =RESOL_TH,
                 RESULTAT=RESOL_TH,
                 OPTION='FLUX_NOEU_TEMP',);

IMPR_RESU(FORMAT='GMSH',
          UNITE=51,
          RESU=_F(RESULTAT=RESOL_TH,
                  NOM_CHAM='TEMP',),);

FIN();

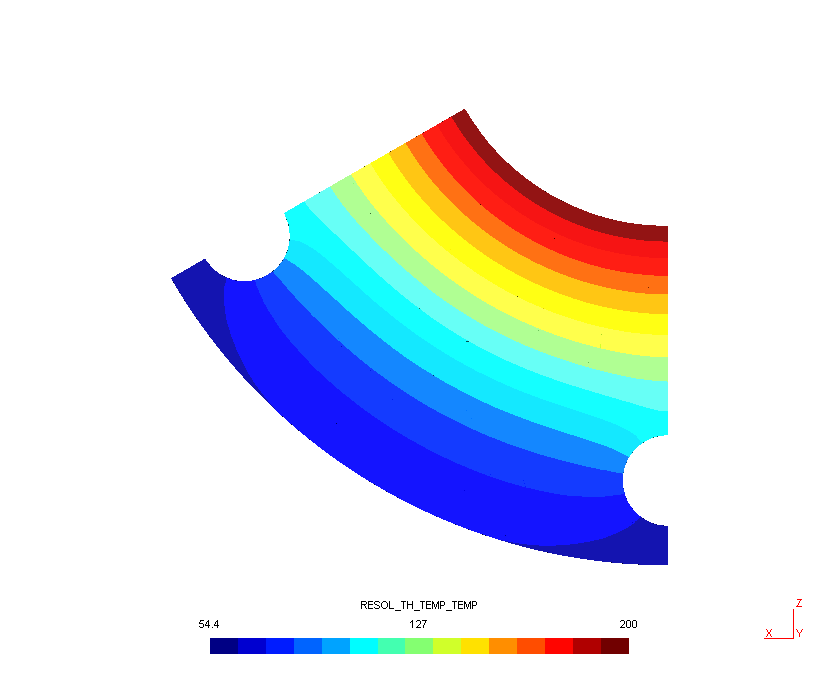
CALC_ELEM et CALC_NO permettent de calculer les températures aux noeuds par extrapolation. L'information est contenue dans FLUX_NOEU_TEMP (flux thermique).

Les figures 1 et 2 présentent le résultat graphique.

**Figure 1:** Cartographie des températures visualisée sous GMSH - vue 1
**Figure 2:** Cartographie des températures visualisée sous GMSH - vue 2

Calcul mécanique - statique

En premier lieu, il est intéressante de mettre visuellement en évidence la transformation d'un maillage quadratique sous gmsh ; la figure 3 montre le maillage avant calcul alors que la figure 4 le montre après calcul¹.

**Figure 3:** Maillage quadratique (hexaèdre) avant calcul
**Figure 4:** Visualisation des éléments après calcul lors d'un post-traitement

En statique linéaire, les grandeurs physiques recherchées sont généralement les isovaleurs de déplacements et les contraintes équivalentes (Von Mises) $\ldots$ des grandeurs scalaires dans les 2 cas. Le fichier de données de Code Aster est de la forme :

POURSUITE();

RESOL_ME=CALC_ELEM(reuse =RESOL_ME,
                   RESULTAT=RESOL_ME,
                   OPTION=('SIGM_ELNO_DEPL','EQUI_ELNO_SIGM',),);

RESOL_ME=CALC_NO(reuse =RESOL_ME,
                 RESULTAT=RESOL_ME,
                 OPTION=('SIGM_NOEU_DEPL','EQUI_NOEU_SIGM',),);

IMPR_RESU(FORMAT='GMSH',
          UNITE=51,
          RESU=_F(RESULTAT=RESOL_ME,
                  NOM_CHAM='EQUI_NOEU_SIGM',
                  NOM_CMP='VMIS',),);

IMPR_RESU(FORMAT='GMSH',
          UNITE=52,
          RESU=_F(RESULTAT=RESOL_ME,
                  NOM_CHAM='DEPL',),);

FIN();

A l'instar du cas précédent, les valeurs de Von Mises extrapolées sont contenues dans EQUI_NOEU_DEPL et VMIS. Les résultats sont générés dans 2 fichiers distincts (un pour les contraintes équivalentes & un pour les déplacements).

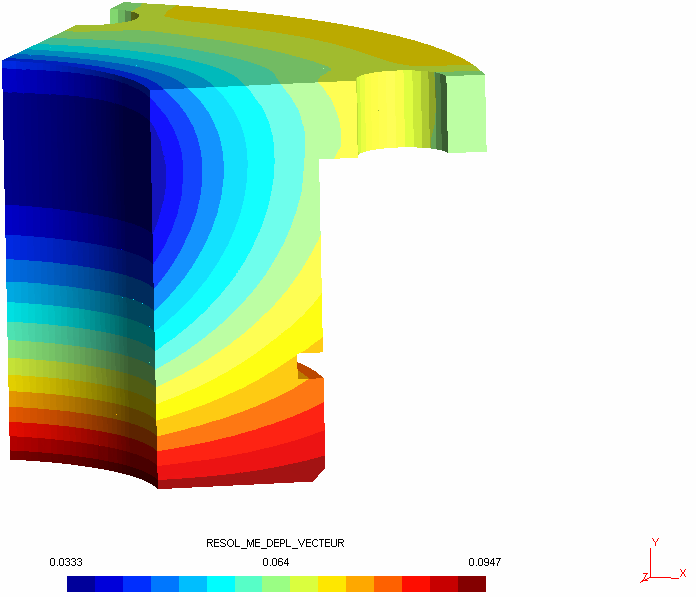
Les figures 5 et 6 présentent les isovaleurs de déplacements ; les 2 suivantes (fig 7 & 8) sont intéressantes parce qu'elles visualisent les vecteurs déplacements.

**Figure 5:** Isovaleurs des déplacements sous GMSH - vue 1
**Figure 6:** Isovaleurs des déplacements sous GMSH - vue 2

**Figure 7:** Vecteurs déplacements sous GMSH - vue 1
**Figure 8:** Vecteurs déplacements sous GMSH - vue 2

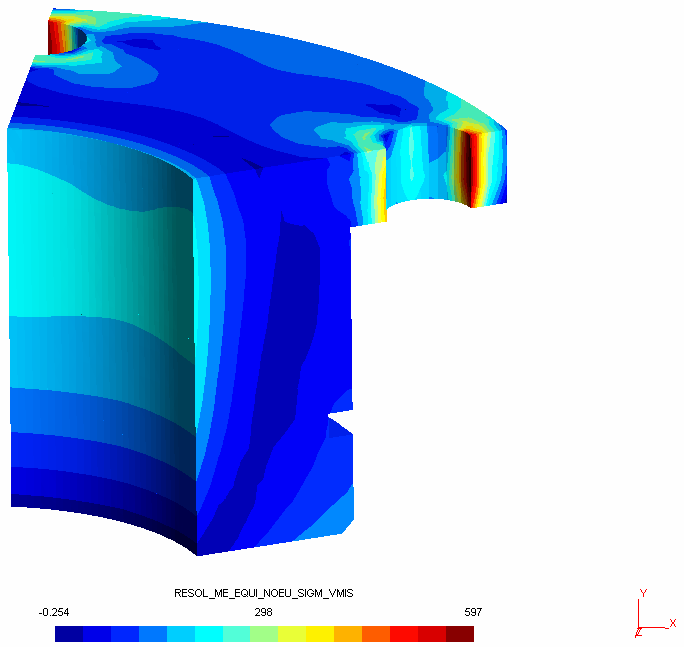
Les cartographies des contraintes sont visibles aux figures 9 et 10.

**Figure 9:** Visualisation des $\sigma _{eq}$ de Von Mises sous GMSH - vue 1
**Figure 10:** Visualisation des $\sigma _{eq}$ de Von Mises sous GMSH - vue 2

Valeurs aux Points d'intégration

A venir dans une prochaine version.

Post-traitements sous GIBI $^{\tiny {\textregistered }}$

GIBI $^{\tiny {\textregistered }}$ est un outil de pré&post-traitement développé par le CEA (Commissariat à l'Energie Atomique) pour CASTEM $^{\tiny {\textregistered }}$ (CAST3M $^{\tiny {\textregistered }}$ ).

Contrairement à GMSH, GIBI $^{\tiny {\textregistered }}$ traite aussi bien les éléments linéaires que les éléments quadratiques ; il permets également de manipuler les grandeurs pour en créer de nouvelles (jusqu'à des calculs complexes). S'il reste un outil puissant, son utilisation est cependant moins intuitive que GMSH.

Le post-traitement se fait en mode console ou au travers d'un fichier ASCII.

AVERTISSEMENT : Nous nous sommes penchés sur l'utilisation de GIBI $^{\tiny {\textregistered }}$ que récemment, aussi nous ne nous plaçons absolument pas ici comme des spécialistes de cet outil ; toute remarque de la part de la communauté visant à améliorer son utilisation est la bienvenue.

Lancement/arrêt de GIBI $^{\tiny {\textregistered }}$

GIBI $^{\tiny {\textregistered }}$ se lance à partir d'un terminal (sous Linux) ou de la même fenêtre DOS que celle servant à lancer Code Aster $^{\tiny {\textregistered }}$ ; la syntaxe est la suivante :

gibi nom_fichier_gibi.extension

Pour passer d'un affichage à un autre, il suffit de cliquer sur l'icône ``Fin trace''. GIBI $^{\tiny {\textregistered }}$ ne donnera la main que lorsque toute les visualisations auront été faites $\ldots$ cela ne signifie pas pour autant que nous seront sortis du module ; pour cela il suffit de taper (en n'oubliant pas le point virgule) :

fin;

Valeurs moyennes aux éléments

A venir dans une prochaine version.

Extrapolation aux noeuds

La mise en données sous GIBI $^{\tiny {\textregistered }}$ fera l'objet d'une section spécifique à l'issue des chapitres suivants.

Mise en données sous EFICAS $^{\tiny {\textregistered }}$

Comme d'habitude, les post-traitements se feront dans un deuxième temps APRES le calcul à proprement parlé.

F comm /symetrie_cyclique_MEC_post.comm D 1
R base /base_MECA D 0
F mess /symetrie_cyclique_MEC_post.mess R 6
F resu /symetrie_cyclique_MEC_post.resu R 8
F erre /symetrie_cyclique_MEC_post.erre R 9
F cast /symetrie_cyclique_MEC_post.cast R 50

Calcul thermique linéaires - stationnaire

Le fichier de post-traitement sous Code Aster $^{\tiny {\textregistered }}$ est de la forme :

POURSUITE();
RESOL_TH=CALC_ELEM(reuse =RESOL_TH,
                   RESULTAT=RESOL_TH,
                   OPTION='FLUX_ELNO_TEMP',);

IMPR_RESU(FORMAT='CASTEM',
          UNITE=50,
          RESU=_F(MAILLAGE=MAIL_TH,
                  RESULTAT=RESOL_TH,
                  NOM_CHAM=('TEMP','FLUX_ELNO_TEMP',),),);
FIN();

A noter que le maillage DOIT ABSOLUMENT être imprimé dans le fichier résultat (cf. MAILLAGE=MAIL_TH,).

Les figures 11 et 12 présentent le résultat graphique.

**Figure:** Cartographie des températures visualisée sous GIBI $^{\tiny {\textregistered }}$ - vue 1
**Figure:** Cartographie des températures visualisée sous GIBI $^{\tiny {\textregistered }}$ - vue 2

Calcul mécanique - statique

Comme il l'a été dit précédemment, GIBI $^{\tiny {\textregistered }}$ prend en compte les éléments quadratiques pour le post-traitement. Par conséquent et contrairement à GMSH, le maillage n'est pas modifié.

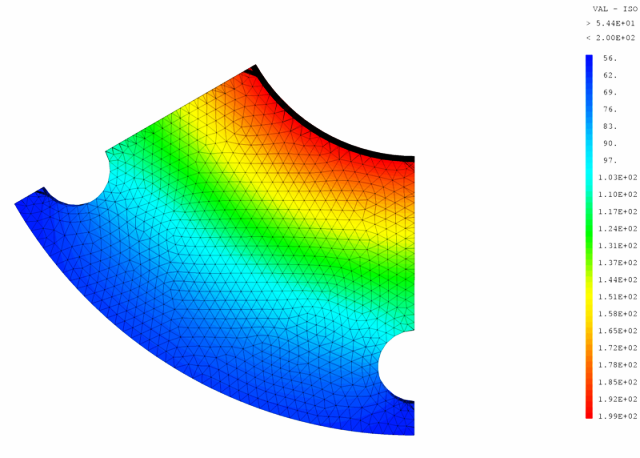
Les déplacements (DEPL) et les contraintes équivalentes (VMIS ou TRES) sont imprimés dans le fichier de Code Aster $^{\tiny {\textregistered }}$ .

POURSUITE();

RESOL_ME=CALC_ELEM(reuse =RESOL_ME,
                   RESULTAT=RESOL_ME,
                   OPTION=('SIGM_ELNO_DEPL','EQUI_ELNO_SIGM',),);

IMPR_RESU(FORMAT='CASTEM',
          UNITE=50,
          RESU=_F(MAILLAGE=MAIL_MEC,
                  RESULTAT=RESOL_ME,
                  NOM_CHAM=('DEPL','EQUI_ELNO_SIGM',),),);

FIN();

A noter que le maillage DOIT ABSOLUMENT être imprimé dans le fichier résultat (cf. MAILLAGE=MAIL_MEC,).

Les figures 13 et 14 présentent les isovaleurs de déplacements ; les 2 suivantes (fig 16 & 17) sont intéressantes parce qu'elles visualisent les vecteurs déplacements.

**Figure:** Isovaleurs des déplacements sous GIBI $^{\tiny {\textregistered }}$ - vue 1
**Figure:** Isovaleurs des déplacements sous GIBI $^{\tiny {\textregistered }}$ - vue 2

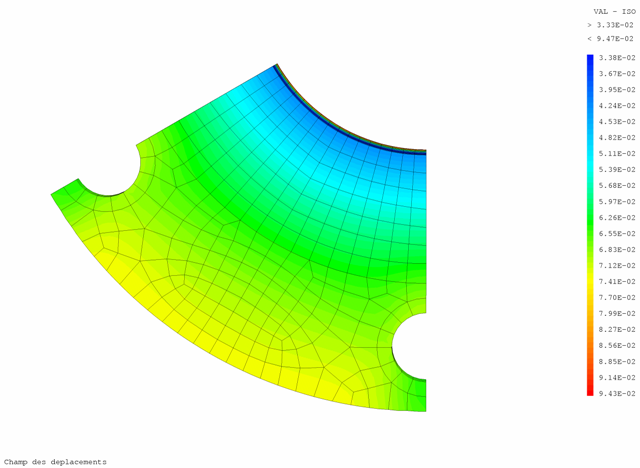
Une fonctionnalité intéressante : il est possible de superposer le maillage déformé sur le maillage initial (cf. figure 15).

**Figure:** Maillage déformé VS maillage initial sous GIBI $^{\tiny {\textregistered }}$ - vue 1

**Figure:** Vecteurs déplacements sous GIBI $^{\tiny {\textregistered }}$ - vue 1
**Figure:** Vecteurs déplacements sous GIBI $^{\tiny {\textregistered }}$ - vue 2

Les cartographies des contraintes sont visibles aux figures 18 et 19.

**Figure 18:** Visualisation des $\sigma _{eq}$ de Von Mises sous GIBI $^{\tiny {\textregistered }}$ - vue 1
**Figure 19:** Visualisation des $\sigma _{eq}$ de Von Mises sous GIBI $^{\tiny {\textregistered }}$ - vue 2

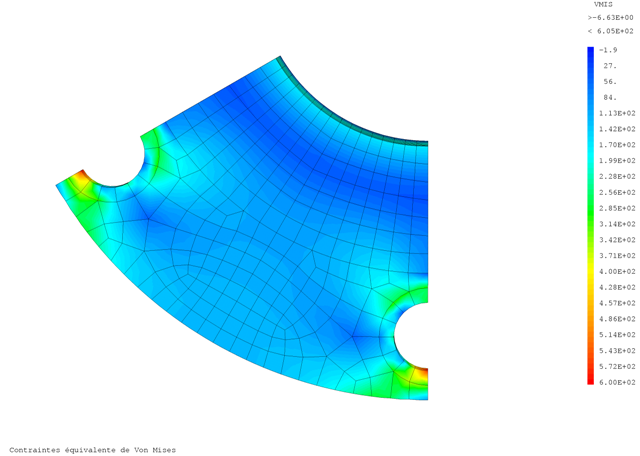
De même, il est possible de visualiser les champs de contraintes sur le maillage déformée (cf. figure 20.

**Figure 20:** Visualisation des $\sigma _{eq}$ de Von Mises sur le maillage déformé (GIBI $^{\tiny {\textregistered }}$ )

Fichier de données GIBI $^{\tiny {\textregistered }}$ pour le calcul thermique

Le fichier ASCII (post_th.cast) de post-traitement est donnée ci-après :

*************************************************************
* donner ici le nom du fichier de post traitement (*.cast)
fich='symetrie_cyclique_TH.cast';

option rest form fich ;
rest form ;

*************************************************************
* donner ici le nom du maillage utilise dans le fichier de
* commandes ASTER et le nom du resultat

maya1 = MAIL_TH ;
res1 = RESOL_TH ;

*************************************************************
list res1.1;

oe1 = 0. -500. 1000. ;
oe2 = 0. 1000. 0. ;
oe3 = 0. 1000. 1000. ;

th1 = res1 . 1 . TEMP ;
temp1 = exco temp th1 ;

postm_th = maya1 elem tet4 ;

titre 'Champ de temperature aux noeuds' ;
trac oe2 temp1 postm_th ;
trac oe1 temp1 postm_th ;

fich, maya1 et res1 sont des variables choisies par l'utilisateur ; chacun est libre de donner le nom qui lui convient. En revanche certains mots clefs sont propres à GIBI $^{\tiny {\textregistered }}$ :

$\triangleright$: list
$\triangleright$: elem
$\triangleright$: mode thermique isotrope
$\triangleright$: trac

Leur signification sera abordée ci-après. Toutes les lignes se terminent obligatoirement par un point-virgule "`;"'. Reprenons pas-à-pas le fichier ASCII :

fich='symetrie_cyclique_TH.cast';

La variable fich qui a été choisie indique à GIBI $^{\tiny {\textregistered }}$ le nom du fichier résultat généré par Code Aster $^{\tiny {\textregistered }}$ ; ce dernier contient le maillage et les grandeurs physiques exportées avec IMPR_RESU.

option rest form fich ;
rest form ;

Ces instructions indiquent à GIBI $^{\tiny {\textregistered }}$ de charger en mémoire les résultats.

maya1 = MAIL_TH ;
res1 = RESOL_TH ;

MAIL_TH est le nom donné au maillage dans le fichier .comm de Code Aster $^{\tiny {\textregistered }}$ (nous lui affectons le nom maya1) et RESOL_TH celui du résultat (nous lui affectons le nom res1). ATTENTION : ces 2 noms doivent être strictement identiques à ceux du fichier .comm définis avec LIRE_MAILLAGE et RESULTAT.

list res1.1;

Cette instruction est équivalente à list RESOL_TH.1 ; le mot clef list est d'une aide précieuse puisqu'il fournit tous les types de résultats présents dans le fichier résultat $\ldots$ concrètement cela signifie que vous ne pourrez pas visualiser une grandeur qui n'est pas listée par cette instruction.

Le .1 signifie qu'il s'agit :

Soit d'un calcul statique (c'est le cas ici);
ou alors qu'il indique le numéro du pas de temps (ici le n $^{\circ}$ 1).

oe1 = 0. -500. 1000. ;
oe2 = 0. 1000. 0. ;
oe3 = 0. 1000. 1000. ;

Les points $oe_{i}$ correspondent à différents centres de visée ; pour info oe signifie oe(il) $\ldots$ mais le lecteur pourra choisir un tout autre nom.

postm_th = maya1 elem tet4 ;

Cette instruction est particulière. En effet comme nombres de modules de post-traitement, il n'est pas possible d'afficher des résultats à la fois sur des éléments de volume (tétraèdres et hexaèdres) et des éléments surfaciques (triangles et quadrangles) ; l'instruction maya1 elem tet4 permet de ne retenir que les tétraèdres linéaires (4 noeuds = tet4) du maillage maya1 $\Rightarrow$ un nouveau maillage post_th est créé.

th1 = res1 . 1 . TEMP ;
temp1 = exco temp th1 ;

th1 pointe sur le champ TEMP du résultat RESOL_TH ; l'instruction exco extrait les températures (temp) de th1. A noter que TEMP figure dans les résultats exportés depuis Code Aster $^{\tiny {\textregistered }}$ (cf. list res1.1).

titre 'Champ de temperature aux noeuds' ;
trac oe2 temp1 postm_th ;
trac oe1 temp1 postm_th ;

Ces dernières instructions sont graphiques : titre'' (sans commentaire) ; trac oe2 temp1 postm_th signifie littéralement "`tracer depuis le point de visée oe2 les valeurs de temp1 sur le maillage postm_th.

Fichier de données GIBI $^{\tiny {\textregistered }}$ pour le calcul mécanique

Le fichier ASCII (post_meca.cast) de post-traitement est donnée ci-après :

*************************************************************
* donner ici le nom du fichier de post traitement (*.cast)
fich='symetrie_cyclique_MEC_post.cast';

option rest form fich ;
rest form ;

*************************************************************
* donner ici le nom du maillage utilise dans le fichier de
* commandes ASTER et le nom du resultat

maya1 = MAIL_MEC ;
res1 = RESOL_ME ;

*************************************************************
list res1.1;

oe1 = 0. -500. 1000. ;
oe2 = 0. 1000. 0. ;
oe3 = 0. 1000. 1000. ;

depl1 = res1 . 1 . DEPL ;

sig_eq1 = res1 . 1 . EQUI_ELNO_SIGM ;

q1 = exco depl1 ux  ;
q2 = exco depl1 uy  ;
q3 = exco depl1 uz  ;

module = ((q1**2) + (q2**2) + (q3**2))**(0.5) ;

post1 = maya1 elem cu20 ;

* visualisation des  deformees 
defo1 = defo maya1 depl1  rouge ;
defo0 = defo maya1 depl1  0. vert ;

titre 'Deformee ' ;
trac oe2 (defo1 et defo0) ;


titre 'Champ des deplacements' ;
trac oe2 module post1 ;

titre 'Visualisation des vecteurs deplacements' ;
VISU_VEC = VECT depl1 100 ;
trac cach oe2 VISU_VEC post1 ;

titre 'Contraintes équivalente de Von Mises' ;
modcast = mode maya1 mecanique elastique  ;
vmi1 = exco vmis sig_eq1 ;
trac oe1 vmi1  modcast  ;
trac oe2 vmi1  modcast  ;
trac oe3 vmi1  modcast  ;

titre 'Contraintes équivalente de Von Mises sur déformée' ;
trac oe1 vmi1  modcast defo1 ;

Le début du fichier reprend la même trame que pour le calcul thermique :

fich='symetrie_cyclique_MEC_post.cast';

option rest form fich ;
rest form ;

Ces instructions indiquent à GIBI $^{\tiny {\textregistered }}$ de charger en mémoire les résultats.

maya1 = MAIL_MEC ;
res1 = RESOL_ME ;

MAIL_MEC est le nom donné au maillage dans le fichier .comm de Code Aster $^{\tiny {\textregistered }}$ (nous lui affectons le nom maya1) et RESOL_MEC celui du résultat (nous lui affectons le nom res1). ATTENTION : ces 2 noms doivent être strictement identiques à ceux du fichier .comm définis avec LIRE_MAILLAGE et RESULTAT.

list res1.1;

Cette instruction est équivalente à list RESOL_TH.1 ; le mot clef list est d'une aide précieuse puisqu'elle fournit tous les types de résultats présents dans le fichier résultat $\ldots$ concrètement cela signifie que vous ne pourrez pas visualiser une grandeur qui n'est pas listée par cette instruction.

Le .1 signifie qu'il s'agit :

Soit d'un calcul statique (c'est le cas ici);
ou alors qu'il indique le numéro du pas de temps (ici le n $^{\circ}$ 1).

oe1 = 0. -500. 1000. ;
oe2 = 0. 1000. 0. ;
oe3 = 0. 1000. 1000. ;

Les points $oe_{i}$ correspondent à différents centres de visée ; pour info oe signifie oe(il) $\ldots$ mais le lecteur pourra choisir un tout autre nom.

depl1 = res1 . 1 . DEPL ;
sig_eq1 = res1 . 1 . EQUI_ELNO_SIGM ;

la variable depl1 pointe sur le champ des déplacement (DEPL) et sig_eq1 sur celui des contraintes équivalentes.

La démarche suivante consiste à extraire les résultats de type Contrainte de Von Mises (VMIS) et les différentes composantes du vecteur déplacement ( $U_{x}$ , $U_{y}$ et $U_{z}$ ) $\ldots$ pour ce faire nous utilisons le mot clef exco :

q1 = exco depl1 ux  ;
q2 = exco depl1 uy  ;
q3 = exco depl1 uz  ;

vmi1 = exco vmis sig_eq1 ;

Pour avoir les isovaleurs de déplacement (champ scalaire), il est nécessaire de calculer le module à partir des composantes du vecteur déplacement ( $\varsigma=\sqrt{q_{1}^{2}+q_{2}^{2}+q_{3}^{2}}$ ).

module = ((q1**2) + (q2**2) + (q3**2))**(0.5) ;

ATTENTION: L'ordre et le nombre de parenthèses n'ont pas été fixés au hasard $\ldots$ ((q1**2) + (q2**2) + (q3**2))**(0.5) donnera un résultat différent de (q1**2 + q2**2 + q3**2)**(0.5) dans le langage GIBIANE (c'est-à-dire de GIBI $^{\tiny {\textregistered }}$ ).

post1 = maya1 elem cu20 ;

Cette instruction est particulière. En effet comme nombres de modules de post-traitement, il n'est pas possible d'afficher des résultats à la fois sur des éléments de volume (tétraèdres et hexaèdres) et des éléments surfaciques (triangles et quadrangles) ; l'instruction maya1 elem cu20 permet de ne retenir que les hexaèdres quadratiques (cube 20 noeuds = cu20) du maillage maya1 $\Rightarrow$ un nouveau maillage post1 est créé.

Le mot clef defo pour (defo)rmation permet de créer un nouveau maillage déformé defo1 en rouge (defo1 = defo maya1 depl1 rouge ;), ou un maillage non deformé en vert (defo0 = defo maya1 depl1 0. vert ;) $\ldots$ A noter le zero (0) qui indique une amplification nulle (ce qui revient au maillage initial). l'instruction trac oe2 (defo1 et defo0) ; demande à tracer le maillage déformé ET le maillage initial grâce à ( . et . ).

* visualisation des  deformees 
defo1 = defo maya1 depl1  rouge ;
defo0 = defo maya1 depl1  0. vert ;

titre 'Deformee ' ;
trac oe2 (defo1 et defo0) ;

titre 'Champ des deplacements' ;
trac oe2 module post1 ;

Il peut être intéressant de visualiser les vecteurs déplacements avec le mot clef VECT (le 100 indique le coefficient d'amplification. Il peut s'avérer utile d'utiliser cach qui n'autorise la visualisation que des éléments de peau (et cach(e)r donc les sous-éléments).

titre 'Visualisation des vecteurs deplacements' ;
VISU_VEC = VECT depl1 100 ;
trac cach oe2 VISU_VEC post1 ;

Quant aux contraintes de Von Mises, il est nécessaire de créer un modèle numérique basé sur le type de calcul. S'agissant d'un calcul statique linéaire s'appuyant sur le maillage maya1, nous créons modcast (modcast = mode maya1 mecanique elastique ;) ; reste à extraite la contrainte équivalente (vmi1 = exco vmis sig_eq1 ;) et à tracer les isovaleurs (trac oe1 vmi1 modcast ;).

titre 'Contraintes équivalente de Von Mises' ;
modcast = mode maya1 mecanique elastique  ;
vmi1 = exco vmis sig_eq1 ;
trac oe1 vmi1  modcast  ;

Post-traitement sous SALOME $^{\tiny {\textregistered }}$

A venir dans une prochaine version.

Post-traitement sous GRACE $^{\tiny {\textregistered }}$

A venir dans une prochaine version.

Conclusion, remerciements, auteur(s)

Droit d'auteur(s) : L'utilisation de ce document sous quelque forme que ce soit est absolument libre au sens que la licence GPL donne à ce terme. Nous souhaitons simplement, si de larges extraits de cette publication sont utilisés dans d'autres documents, qu'il soit fait mention du nom du(des) auteur(s) du document initial.

Remerciements : L'auteur(s) souhaite(nt) remercier les personnes de la communauté de Code Aster $^{\tiny {\textregistered }}$ et de Cast3M $^{\tiny {\textregistered }}$ qui ont fourni aides et informations précieuses : qu'ils en soient chaleureusement remercier. L'ensemble des notes présentes sur le site ne sont que la continuation de cet esprit "libre" qui vise entre-autres choses partager son savoir et son travail $\ldots$

L'auteur : Paul CARRICO².

Les commentaires sont à adresser à :

paul.carrico_at_free.fr

À propos de ce document...

Tutorial 1 :
Post-traitements des résultats
Utilisation des outils connexes à Code Aster $^{\tiny {\textregistered }}$
Version 1

This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)

The command line arguments were:
latex2html -split 0 CAELINUX_post-traitement.tex

The translation was initiated by on 2007-02-21

Notes

... calcul ¹: loin de nous de critiquer cette méthode qui est liée aux limitations de GMSH, nous pensons qu'il faut juste en avoir conscience.
... CARRICO ²: Avant de travailler sur des outils propriétaires, j'ai fait mes premières armes sur Code Aster $^{\textregistered}$ que j'utilise encore ponctuellement. Ces tutoriaux sont pour moi l'occasion de coucher sur le papier une démarche (pas nécessairement exhaustive) qui est la mienne à la fois pour la partager et l'améliorer/corriger au grès des retours, et l'occasion de garder la main sur un code que considère comme rigoureux (par opposition aux boîtes noires qui fleurissent depuis un certain nombre d'années).

2007-02-21

Tutorial 1 : Post-traitements des résultats Utilisation des outils connexes à Code Aster Version 1

Notes

Tutorial 1 :
Post-traitements des résultats
Utilisation des outils connexes à Code Aster $^{\tiny {\textregistered }}$
Version 1